Dois condutores e no vácuo são conectados diretamente a uma bateria cuja força eletromotriz é igual a , conforme mostra a figura. Uma das linhas de campo elétrico originadas pela configuração está alinhada com o eixo entre os pontos e da superfície dos condutores.
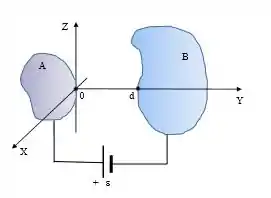
Ao longo desta linha, o campo é dado pela função:
onde é uma constante e é a carga (desconhecida) do condutor positivo. Determine:
(a) A carga com sinal dos condutores e , em função dos parâmetros da configuração (;
(b) A capacitância da configuração, em função dos mesmos parâmetros;
(c) A energia fornecida pela bateria, em função dos mesmos parâmetros;
(d) Se o vácuo é substituído por um meio de constante dielétrica igual a enquanto a conexão da bateria com os condutores é mantida, recalcule os itens (a), (b) e (c);
Em uma fase posterior, a bateria é removida e substituída por um resistor de resistência . Nesta condição, determine:
(e) A corrente no resistor em função do tempo;
(f) A ddp em função do tempo;
(g) A potência dissipada no resistor no início desta fase.
Passo 1
a) Sabemos que:
No entanto, para esse caso:
Integrando:
E então:
Passo 2
b) Para encontrar a capacitância, basta usarmos que:
E então:
Passo 3
c) A energia armazenada em um capacitor é dada por:
Portanto, neste caso:
Passo 4
d) A única mudança é a permissividade do meio, que agora será dada por , então:
Passo 5
e) Sabemos que, em um circuito RC, a corrente é dada por:
E também que:
Portanto:
Passo 6
f) A ddp é dada por:
E:
Logo:
Passo 7
g) Sabemos que:
Mas a corrente no início é dada por:
Portanto:
Resposta
(a) e
(b)
(c)
(d)
(e) A;
(f)
(g)