UFJF – Física 3 – AV3 – 2ª CH – 2016.2 – Questão 3
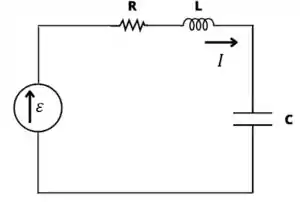
A figura abaixo mostra um circuito com uma fonte de voltagem alternada com força eletromotriz .Esta fonte de voltagem tem a frequência regulável. No regime estacionário se observou que a corrente fica em fase com a força eletromotriz quando a frequência da fonte tem o valor de . Não é fácil verificar se a corrente oscila exatamente em fase com a voltagem. Por esta razão a pessoa que fez a medida estimou uma incerteza deste valor de . O valor da capacitância vale e o valor da resistência vale . Determine o valor da indutância do circuito assim como a incerteza experimental deste valor.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá um circuito e nos pede para calcular a indutância e a incerteza causada por conta da oscilação da corrente.
Como trata-se de um circuito em corrente alternada, vale lembrar as seguintes fórmulas de reatância capacitiva e indutiva :
Mas como podemos aplicar isso?
E aí? Bora responder?
Passo 2
Bom... quando a questão fala que a tensão e a corrente estão em fase, isso significa que as reatâncias capacitiva e indutiva são numericamente iguais, ou seja:
Assim, sabendo que , podemos isolar a indutância :
Passo 3
Assim, a partir dessa expressão, podemos calcular os seguintes valores:
- Valor base:
- Valor mínimo:
- Valor base:
Assim, temos que
Passo 4
Além disso, podemos calcular a incerteza :
Entendeu direitinho? Responde aee ;)
