3ª questão - Na figura abaixo, os 4 capacitores estão completamente carregados. Determine a energia armazenada por , sabendo que , , , e .
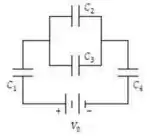
A)
B)
C)
D)
E)
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍

Nessa questão temos um circuito com 4 capacitores e uma fonte de . A capacitância de cada capacitor foi dada no enunciado, mas o que queremos saber é a energia armazenada no capacitor visto que todos os capacitores estão carregados.
Então, tem ideia de como fazer isso? 🤔🤔
A energia armazenada em um capacitor é dada por
Já temos , então temos que encontrar a tensão no capacitor .
Entendeu? Bora pra cima! 😁
Passo 2
Primeiro de tudo, temos que obter a capacitância equivalente do circuito, lembra como faz?
Capacitor em paralelo a gente soma como resistores em série, em série a gente calcula como capacitores em paralelo.
Por exemplo, o conjunto de e resulta em um capacitor equivalente de , ou seja,
Agora perceba que , e estão em série, logo a capacitância equivalente é dada como
Isso resulta em
Logo a capacitância equivalente do circuito é
Agora usamos essa informação para calcular a tensão em .
Quer ver? Bora lá!
Passo 3
A tensão em será dada como
Sabendo que é igual a , é igual a e é igual a , temos que
Com isso, descobrimos que a tensão em é de .
Substituindo em que mostramos no passo 1, temos
Logo, vemos que a energia armazenada em é dada por
Ou seja, a alternativa que condiz com o resultado que encontramos é a alternativa D)!
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí

Resposta
D)