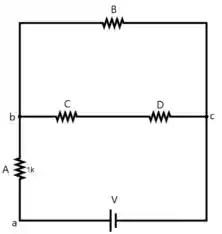
1- Na figura ao lado, uma fonte de e quatro lâmpadas idênticas , , e são arranjadas de acordo com o circuito fornecido. Supondo que o brilho das lâmpadas seja proporcional à sua potência dissipada, liste as lâmpadas em ordem decrescente de brilho.
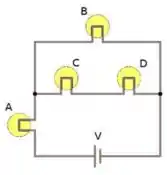
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Nesse problema, temos um circuito formado por lâmpadas iguais e de acordo com a distribuição dessas lâmpadas pelo circuito, temos que ranqueá-las em ordem decrescente de brilho.
Tem ideia de como fazemos isso? 🤔
O brilho de uma lâmpada é proporcional à potência dissipada por ela.
Pela lei de Ohm, sabemos que a potência dissipada é dada por
Ou pela relação , podemos dizer que ou , então tendo a tensão ou a corrente da lâmpada, podemos definir qual tem o maior brilho.
Sacou? Bora começar! 😁
Passo 2
Vamos começar montando o circuito equivalente substituindo as lâmpadas por resistências
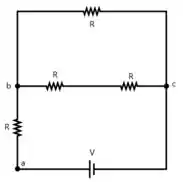
Associando as resistências em serie entre os pontos e , temos
Substituindo no circuito equivalente...
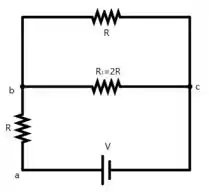
Tranquilo até aqui? 👀
Passo 3
Agora temos que fazer a associação em paralelo dos resistores entre os pontos e
Substituindo no circuito novamente...
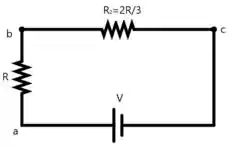
Agora que temos apenas uma malha no circuito, podemos aplicar o método de divisão de tensão para obter as tensões entre os pontos e e entre e .
Assim, como a distribuição de tensão é linear, a tensão entre e é dado por
Entendeu essa parte? 😐
Passo 4
Por fim, vamos analisar a distribuição de tensão no circuito.
Sabemos que a tensão entre os pontos e é de e entre e é .
Como vimos anteriormente, o brilho será proporcional a tensão sobre eles, então, vemos que só na lâmpada a tensão é exatamente a mesma tensão , ou seja
Já na lâmpada , a tensão será a mesma tensão já que seus terminais estão ligados a esses pontos diretamente.
Agora para as lâmpadas e , podemos aplicar o método de divisão de tensão novamente, ou podemos pensar de maneira mais física...
e estão ligados em serie e possuem a mesma resistência, portanto, a tensão será dividida igualmente para e para , como se elas estivessem dividindo as tensões de maneira igualitária entre elas. Com isso, podemos definir que
E finalmente, colocando em ordem decrescente de brilho, temos
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
