Um capacitor de capacitância está ligado em paralelo a um resistor de resistência , conforme a figura. No instante a carga do capacitor é e a chave é fechada.
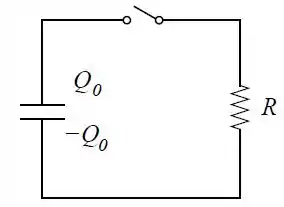
Escreva a equação diferencial para a carga na placa superior do capacitor para .
Calcule e para .
Calcule a energia armazenada no capacitor. Note que não é constante. Calcule e interprete o resultado.
Passo 1
Escreva a equação diferencial para a carga na placa superior do capacitor para .
Aqui, o potencial fornecido pelo capacitor deve ser totalmente dissipado no resistor, logo:
Lembrando que, durante a descarga de um capacitor, , teremos:
Passo 2
Calcule e para .
A solução geral para esse tipo de problema tem a cara:
O problema nos disse que, em , a carga no capacitor é , logo:
Sendo assim:
Uma vez que encontramos a expressão para , para encontrarmos a expressão de basta fazer . Portanto:
Passo 3
Calcule a energia armazenada no capacitor. Note que não é constante. Calcule e interprete o resultado.
A energia armazenada no capacitor é dada por:
Substituindo a expressão de que encontramos no item anterior, teremos:
Finalmente:
Passo 4
Uma vez que encontramos a expressão de , agora a nossa vida ficou um pouco mais tranquila.
Organizando esse cara, teremos:
Concorda que tem, necessariamente, unidade de potência?
Então vamos calcular a potência dissipada no resistor e comparar com a expressão acima, ok?
Opa! Conseguiu ver que:
Isso significa que a variação de energia no capacitor é igual à potência dissipada no resistor.
Resposta