Todos os elementos do circuito da Figura ao lado são conhecidos. Inicialmente, os capacitores e estão descarregados e a chave aberta.
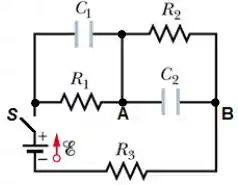
a) Determine a corrente na bateria (indicando seu sentido) imediatamente após o fechamento da chave .
b) Determine a corrente na bateria (indicando seu sentido) muito tempo após o fechamento da chave .
c) Determine as tensões nos capacitores e (indicando seus sentidos) muito tempo após o fechamento da chave , assim como as energias neles armazenadas.
d) Após os plenos carregamentos dos capacitores, a chave e a bateria são substituídas por um curto e o capacitor é retirado do circuito e no seu lugar nada é colocado. Determine a resistência equivalente observada a partir dos terminais A e B. Em seguida, caracterize totalmente a corrente no capacitor em função do tempo (indicando seu sentido).
Passo 1
Cara... Nesse problema aqui, temos que ter em mente de que o capacitor em fontes de corrente contínua tem três momentos interessantes:
- No primeiro momento quando a chave é ligada, o capacitor puxa o máximo de corrente pra ele se recarregar, em outras palavras, o capacitor atua como um curto-circuito:
- O segundo momento, conhecido como período de transitório, acontece quando o capacitor está sendo carregado.
- E o terceiro e último momento, é chamado de momento estacionário, que é quando o capacitor já se carregou completamente e cessa a corrente que passa nele, ou seja, ele se transforma em um circuito aberto:
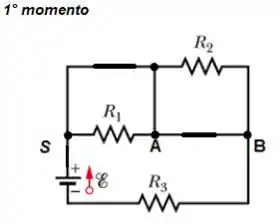
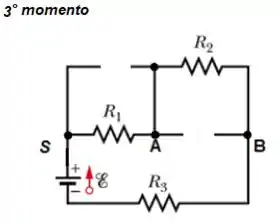
Passo 2
O problema nesse item nos pede a corrente da fonte imediatamente após a chave se fechar, ou seja, ela quer a corrente da fonte no momento...
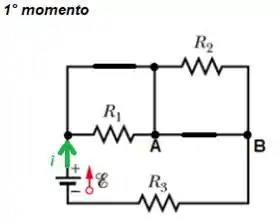
POW! Então para encontrar a corrente temos que resolver esse circuito!
Mas olha que massa esse circuito! A corrente não vai passar pelo resistor e nem pelo resistor nesse primeiro momento! Afinal, a corrente sempre dá preferência para o caminho de menor resistência! Como o curo circuito é considerado como resistência , então é por ele que a corrente passa!
Se a corrente não passa nem pelo resistor e nem pelo resistor a gente pode eliminá-los da brincadeira...
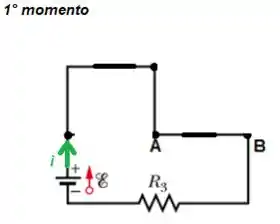
Pela Lei das Malhas, a da fonte é a tensão em cima do único resistor que sobrou no circuito, isto é...
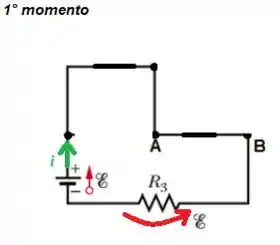
Então, pela Lei de Ohm...
Então essa é a corrente que passa na fonte assim que a chave se fechar. Por se tratar de uma corrente momentânea (que acontece apenas no momento inicial), vou chamar de corrente ...
Passo 3
Neste item, opostamente ao item , vamos trabalhar com o circuito no terceiro momento, ou seja, quando tiver se passado muito tempo após a bateria tiver se logado...
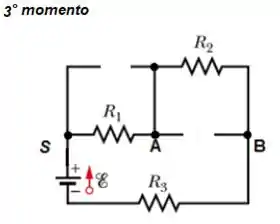
E vamos determinar a corrente nesse momento...
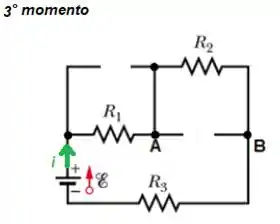
Para determinar essa corrente, veja que os três resistores estão em série entre si. Então, a resistência total será...
A corrente que sai da fonte então será pela Lei de Ohm...
Portanto...
Como essa corrente é a corrente de estado final que passa pelo circuito, vou chama-la de ...
Passo 4
Novamente nesse item, estamos falando do circuito no terceiro momento...
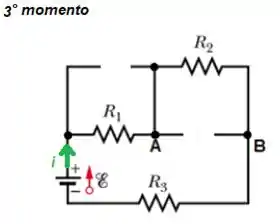
Repare que o resistor está em paralelo com o capacitor de cima, portanto a tensão em cima do capacitor , será a tensão em cia do resistor ...
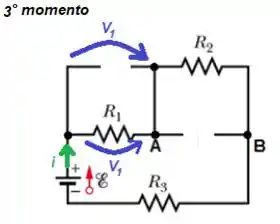
E para o , o capacitor está em paralelo com o resistor de modo que...
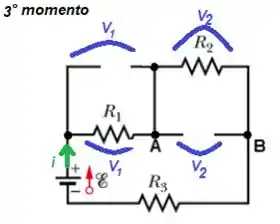
Então, para encontrar as tensões em cima dos capacitores, precisamos determinar as tensões em cima dos resistores. Ora... A corrente é a corrente que passa por todos os resistores (já que todos estão em série), então, pela Lei de Ohm...
Passo 5
Tensões encontradas, podemos determinar a energia armazenada em cada capacitor pela fórmula...
Então a energia em cima do capacitor será...
E para o capacitor ...
Passo 6
Bem, nesse problema da letra , após os capacitores estarem plenamente carregados, alguém vai lá no circuito e modifica a estrutura original dele, colocando um curto na fonte e na chave e removendo o capacitor ...
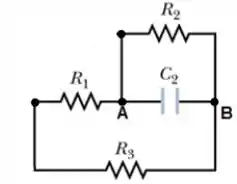
Como o capacitor está ainda conectado (e completamente carregado), vai surgir uma corrente indo para os resistores...
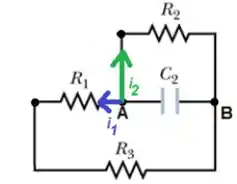
POW! Repare que a resistência e é percorrida pela mesma corrente , ou seja, essas duas resistências estão em série...
Só que o ramo de baixo está em paralelo com o ramo de cima (ramo da resistência ), então a resistência final vista pelo capacitor () vai ser o paralelo de com a resistência série...
Então, pela regra de paralelo...
Então essa é a resistência total vista pelo capacitor. É como se pudéssemos substituir todos esses resistores aí por um único resistor conectado com o capacitor de valor .
Passo 7
Bem, o problema também pede para caracterizarmos a corrente que circula no capacitor . Para isso, precisamos saber o módulo da corrente .
Pow! De acordo com a teoria, a corrente que surge no capacitor será...
Como ...
E o é a tensão no indutor no momento em que tudo se desconecta...
Resposta
Letra A:
Letra B:
Letra C:
Letra D: