Na figura abaixo, a força eletromotriz da fonte ideal é , as resistências são e e o capacitor de capacitância está inicialmente descarregado. A chave é fechada em .
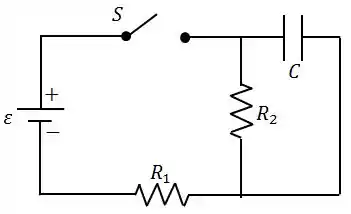
Determine, imediatamente após o fechamento de :
A corrente no resistor 1;
A corrente no resistor 2;
Transcorrido um tempo muito longo após o fechamento de , qual é a carga do capacitor?
Abrindo-se agora a chave , determine a corrente em em função do tempo;
Passo 1
A corrente no resistor 1;
Imediatamente após o fechamento da chave, a carga no capacitor é nula, assim a diferença de potencial no capacitor também será nula.
Assim, através da lei das malhas, percorrendo a malha que contém a fonte, o capacitor e a resistência , teremos:
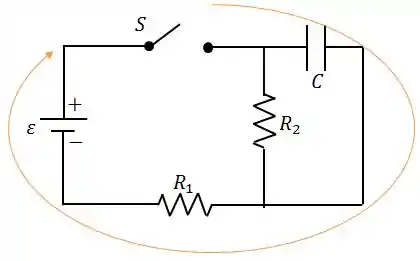
Logo:
Passo 2
A corrente no resistor 2;
Novamente, vamos usar a lei das malhas, mas agora percorrendo a malha que contém somente o capacitor e o resistor .
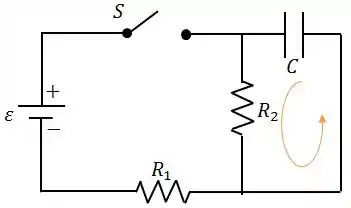
Como falamos no passo anterior, assim que a chave é fechada, a carga no capacitor é nula, logo:
Passo 3
Transcorrido um tempo muito longo após o fechamento de , qual é a carga do capacitor?
Quando , o capacitor fica completamente carregado. Nessa situação, não passa mais nenhuma corrente pelo capacitor, que passa a circular apenas por .
Como e estão em paralelo, a diferença de potencial entre os dois deve ser a mesma. Assim, vamos começar calculando a diferença de potencial em .
Onde é a corrente quando .
Assim, percorrendo a malha que contém , e , teremos:
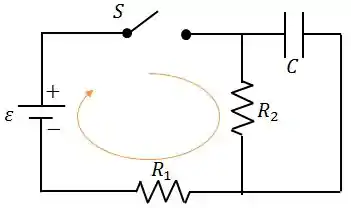
Portanto:
Novamente, como a diferença de potencial em deve ser igual à diferença de potencial no capacitor, teremos:
Finalmente:
Passo 4
Abrindo-se agora a chave , determine a corrente em em função do tempo;
Quando abrimos a chave, o capacitor começa a descarregar, e o circuito fica resumido a:
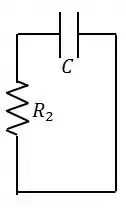
Durante o descarregamento do capacitor, a corrente é dada por:
O sinal negativo aparece mostrando que a corrente, agora, vai circular o sentido contrário ao da corrente durante o carregamento.
Caso você não lembre da expressão da corrente de cabeça, ela é encontrada resolvendo-se a equação diferencial:
Resolvendo essa equação diferencial, encontraremos uma expressão para a carga no capacitor .
Para encontrar a expressão para a corre, basta derivar esse cara em função do tempo:
Resposta