Considere o circuito RC da figura, onde , , é um capacitor de placas paralelas de área , com separação de , tendo um meio entre as placas de constante dielétrica , e . e são duas chaves.
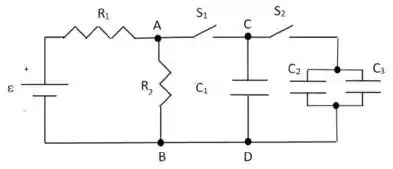
Todos os capacitores estão inicialmente descarregados. Neste circuito, ocorrem as seguintes fases sucessivas:
Fase 1: chave fechada e aberto durante longo tempo.
Fase 2: chaves e abertas e o dielétrico substituído por outro de .
Fase 3: chave aberta e fechada.
Fase 4: chaves e fechadas.
Determine:
- A capacitância .
- As correntes em e no instante inicial da fase 1.
- A energia armazenada em e a potência dissipada em no final da fase 1.
- O trabalho externo necessário para substituir o meio dielétrico na fase 2.
- A diferença de potencial no final das fases 1, 2 e 3.
- A corrente em (sentido e intensidade) no início da fase 4.
Em todos os cálculos, considere .
Passo 1
a) Aqui é importante se lembrar que, quando um dielétrico (um material isolante!) é inserido no interior de um capacitor, a sua capacitância aumenta, já que essa nova capacitância é igual a anterior multiplicada por um número , que é a mesma coisa que escrever o seguinte:
Como e , temos
Passo 2
b) Como os capacitores começam descarregados, no instante inicial da fase 1, em que a chave está fechada, o capacitor ainda não tem carga, ou seja, . Como a diferença de potencial do capacitor é:
Como esse capacitor está em paralelo com o resistor , a ddp entre os pontos e também é zero, ou seja, os pontos e tem o mesmo potencial. Nesse caso, é comum dizer que o capacitor é equivalente a um “curto circuito”.
Como não tem ddp entre A e B, então não pode passar corrente no resistor , porque senão haveria uma queda de potencial nele. Por isso, o que devemos ter é:
A corrente que passa no resistor passa através do capacitor . Essa corrente tem valor:
Passo 3
c) No final da fase 1, o capacitor está totalmente carregado e através dele já não passa nenhuma corrente elétrica. A corrente elétrica que vai ter nesse circuito agora passa pelos resistores e que estão em série.
Primeiro, vamos encontrar essa corrente que passa nesses resistores. Essa corrente será:
A potência dissipada no resistor será, então,
Como o capacitor está em paralelo com o resistor , sua diferença de potencial é:
Com isso, podemos calcular a energia armazenada em :
Passo 4
d) A fase 2 começa com a abertura da chave . No final da fase 1, o capacitor foi carregado completamente e a carga que ele tem no início da fase 2 é:
Fica ligado!! Essa é a carga que o capacitor tem nas duas situações com os dielétricos diferentes. Guarda isso, porque a gente vai usar isso para matar este item…
Mas aí, você me pergunta: “mas, então, o que está variando quando a gente troca o dielétrico na fase 2?” Bom, o que muda nesse caso é a capacitância do capacitor! A nova capacitância na fase está relacionada com a nova constante dielétrica . Com isso, fica:
Nessa expressão, a gente relacionou a nova capacitância na fase 2, com a capacitância anterior da fase 1, beleza? Isso facilita, porque já sabemos que: .
Agora, o trabalho que é gasto, ou seja, a energia que é gasta para trocar o dielétrico para o novo dielétrico é igual a diferença entre a nova energia com o novo dielétrico e a energia com o dielétrico antigo:
Como , temos que o trabalho fica:
Como o capacitor tem energias diferentes com cada um dos dielétricos, o que sobra dessa diferença energia é o que é gasto para inserir o novo dielétrico, ou seja, o trabalho .
Passo 5
e) No final da fase 1: o capacitor está totalmente carregado, por isso, temos que a ddp entre e será igual a:
que é o resultado que encontramos no item c.
No final da fase 2: a nova capacitância com a mudança de dielétrico é . Então:
No final da fase 3: quando a chave é fechada, os capacitores e a capacitância equivalente entre e estão em paralelo, já que e estão submetidos à mesma ddp .
A capacitância equivalente é:
A capacitância equivalente total será:
Como a quantidade carga nessa associação é a mesma que o capacitor tinha no final da fase 2, então:
Passo 6
f) No início da fase 4, em que ambas as chaves estão fechadas, temos que a ddp entre A e B é igual a ddp entre C e D, que é , que acabamos de calcular no Passo 5. Por isso
Vamos supor que a corrente que passa no resistor está no sentido horário. Aplicando a lei das malhas para a malha que contém esse resistor, temos:
Como a corrente é positiva significa que escolhemos o sentido corrente para ela no circuito. Portanto, seu sentido é horário.