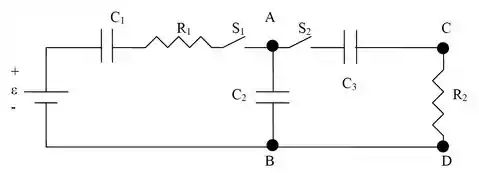
No circuito abaixo os capacitores e estão inicialmente descarregados e ocorrem as seguintes fases sucessivas:
Fase 1: chave fechada e aberta durante longo tempo;
Fase 2: chave abertas e o meio de substituído por outro de constante dielétrica vezes menor;
Fase 3: chave aberta e fechada durante longo tempo.
Considerando , determine com justificativa:
A corrente elétrica em função do tempo em durante a fase .
A energia dissipada em na fase .
A energia fornecida pela bateria na fase .
A d.d.p. no final da fase .
A energia armazenada em na fase .
A d.d.p. no início e final da fase .
As cargas em no final da fase .
Passo 1
Vamos primeiramente analisar a fase , durante essa fase, temos que os capacitores e , inicialmente descarregados irão se carregar. Sempre que temos um capacitor carregando, temos que a corrente varia da seguinte maneira:
Onde é a chamada constante de tempo capacitiva! Repare, que temos nesse caso dois capacitores em série, portanto, é a capacitância equivalente e vale:
Ou seja, a constante de tempo capacitiva é:
Sabendo que e , temos que a corrente varia com o tempo da seguinte forma:
Passo 2
Como já sabemos como a corrente no resistor varia em função do tempo, podemos calcular a energia dissipada da seguinte forma:
No caso, pela corrente variar com o tempo, temos:
Substituindo, temos:
Molezinha!
Passo 3
Podemos determinar a energia fornecida pela bateria usando o mesmo mimimi que usamos no item anterior, se liga!
Como temos que a corrente varia com o tempo, vai rolar uma integralzinha aqui também!
Substituindo, temos:
Passo 4
Para determinar a d.d.p no final da fase , precisamos lembrar da seguinte relação:
Para , teremos:
Nós já sabemos quanto vale a capacitância , precisamos apenas determinar a carga total armazenada . Para isso, podemos pensar da seguinte forma, quando temos dois capacitores em série, temos que ambos devem armazenar a mesma carga , caso contrário, as cargas iriam se “mover” até atingir esse equilíbrio! Além disso, essa é a mesma carga que é armazenada no capacitor equivalente, se liga:
Agora é só substituir para achar , temos:
Passo 5
Agora que já temos a carga armazenada no capacitor ao fim da fase , fica fácil determinar a energia armazenada!
Para a energia armazenada em , temos:
Passo 6
No início da fase , teremos que o capacitor , que está carregado, terá uma nova capacitância, por conta do dielétrico, ou seja, a d.d.p entre seus terminais será diferente. Além disso, temos que o capacitor estará descarregado, ou seja, a d.d.p entre seus terminais será nula.
Como queremos calcular a d.d.p nos terminais do resistor , e sabemos que , basta calcular , pois. Para isso, vamos começar calculando o no valor da capacitância:
Como temos a carga armazenada no capacitor, podemos determinar , se liga!
Ou seja:
No final da fase , o circuito entra em equilíbrio, ou seja, os capacitor vai descarregar parcialmente, enquanto o capacitor irá carregar até que ambos atinjam um valor de carga, a partir do qual a corrente para de fluir no circuito, ou seja , então:
Passo 7
No final da fase , teremos que o capacitor continua com sua carga armazenada durante a fase :
Para determinar as cargas dos capacitores e , devemos pensar na conservação da carga, no início da fase , o capacitor tinha carga , enquanto que o capacitor estava descarregado, pela conservação, temos:
Além disso, temos:
Como a d.d.p será a mesma, temos:
Substituindo na equação da conservação, temos:
Para , temos:
Uffaaa....Cabô!
Resposta
;
; ;