O interruptor do circuito abaixo ficou por longo tempo na posição . Foi trocado para a posição em .
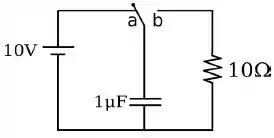
Qual é a carga no capacitor no tempo ?
Passo 1
Como o problema fala que a chave ficou muito tempo na posição , partimos do princípio que o capacitor está totalmente carregado.
Quando a chave muda para a posição , o capacitor passa a funcionar como fem, e vai tendo a sua energia dissipada no resistor. Durante a descarga do capacitor, a carga varia com o tempo da seguinte forma:
Onde , logo:
Assim, para , teremos que: