Física 2 - UFF; P3 de 2019.1
5 - Um capacitor de é conectado a uma fonte cuja fem aumenta uniformemente com o tempo a uma taxa de . A corrente de deslocamento entre as placas é:
- .
Passo 1
Primeiro acho interessante começarmos esse problema desenhando o circuito: capacitor ligado uma fem (‘fonte’):
Quando a tensão vai aumentando, vai gerando uma diferença de potencial crescente no capacitor e com isso um campo elétrico entre as placas que também aumentam:
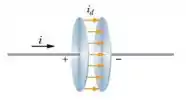
Isso provoca a ida de mais corrente para o capacitor para aumentar a carga dele e assim aumentar o campo elétrico. É como se ele tivesse carregando, saca?
Essa corrente que vai para o capacitor fica estagnada nas placas aumentando o campo, mas é como se ela atravessasse mantendo a corrente! Essa é a corrente de deslocamento, saca? ! E a gente pode a encontrar assim:
Onde é a tensão que está aumentando com o tempo!
Passo 2
No nosso caso, foi dito que a tensão aumenta em uma taxa de . Essa é a taxa de variação dela. Como sabemos do cálculo, taxa de variação nada mais é que a derivada:
Como a capacitância é , a corrente de deslocamento (corrente fictícia que atravessa o capacitor) é então:
Resposta
Letra E.