Duas placas paralelas condutoras de área , separadas de uma distância pelo meio dielétrico de permissividade elétrica , constituem um capacitor cuja capacitância aproximada é dada por:
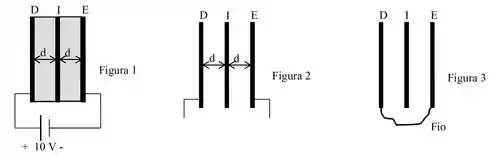
Baseado nisso, considere a configuração da Figura , constituída de uma bateria e três placas paralelas condutoras de determinada espessura não desprezível e equivalente a uma combinação de dois capacitores. As placas estão inicialmente descarregadas, têm áreas iguais a cada uma e estão separadas de por meios dielétricos iguais de constante dielétrica . (Nos cálculos, utilize: )
Considere as seguintes fases sucessivas:
Fase :
As placas e são conectadas a uma bateria de fem igual a , conforme a Figura . Nesta situação, determine:
As cargas elétricas, com sinais, das placas , e .
A energia total armazenada nas regiões entre as placas.
Fase :
A bateria é removida e, a seguir, os meios dielétricos entre as placas são substituídos pelo vácuo, conforme mostra a Figura . Nesta situação determine:
As d.d.p entre as placas: , e .
O trabalho externo necessário para remover os dielétricos.
Fase :
As placas e são conectadas entre si durante longo tempo por um fio com resistência de , conforme mostra a Figura . Nesta fase, determine:
A intensidade e o sentido da corrente elétrica no fio em função do tempo.
A energia dissipada no fio
A carga elétrica das placas ao final desta fase.
Passo 1
Para determinar as cargas elétricas das placas, vamos primeiro achar o valor da capacitância, temos dois capacitores idênticos ligados em série, a capacitância de cada um deles é:
Lembre-se de usar as unidades no S.I!
Agora que temos a capacitância, vamos calcular a capacitância equivalente dos capacitores em série:
A carga de cada placa será dada pela seguinte relação:
Pelo desenho, vemos que as cargas positivas irão se acumular na placa , enquanto as negativas irão se acumular na placa , permanecendo a placa sem carga! As cargas ficam então:
Passo 2
A energia armazenada entre as placas é dada pela seguinte fórmula:
Substituindo, temos:
Lembre-se que temos de usar a capacitância equivalente!
Passo 3
Ao retirar a bateria, as placas irão continuar com a mesma carga, por conta da conservação. Além disso, quando retiramos os dielétricos, temos que calcular a nova capacitância do arranjo. Ela será dada por:
Ao tirarmos o dielétrico de constante , devemos apenas dividir a capacitância pela constante. Tá lembrado que no item a gente teve que multiplicar?!
Como sabemos que a carga permanece constante, temos que as diferenças de potencial serão:
Entre as placas e
Portanto, entre as placas e , e e , temos:
Passo 4
Para determinar o trabalho realizado para retirar o material dielétrico, precisamos calcular a energia armazenada na nova configuração e retirar a energia armazenada na configuração antiga, ainda bem que já calculamos isso no item .
O trabalho será:
Passo 5
A situação descreve um circuito RC, nesse tipo de circuito, quando o capacitor descarrega, temos que a corrente é dada pela seguinte fórmula:
Onde é a d.d.p, é a resistência e , substituindo os valores, temos:
A corrente irá circular da placa em direção a placa .
Passo 6
Ao descarregar totalmente, toda a energia armazenada no capacitor é dissipada pelo fio, desse modo, temos que a energia dissipava é:
Passo 7
Após descarregar totalmente as placas e passaram a ter carga nula, enquanto que a placa , que já tinha carga nula, permanecerá assim!
Resposta
; ;
;
;