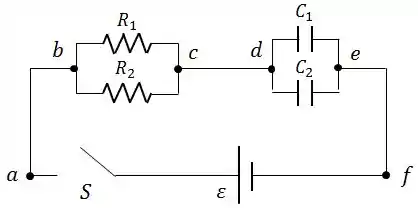
O circuito da figura contém dois resistores e e dois capacitores e e o conjunto é ligado a uma bateria de . Antes de a chave ser ligada, os capacitores estão descarregados.
determine a constante de tempo desse circuito;
determine a corrente que atravessa a bateria em função do tempo após o fechamento da chave ;
determine a entre os ponto e em função do tempo;
com fechada por um longo tempo, quais são as cargas nos capacitores e .
Passo 1
determine a constante de tempo desse circuito;
Antes de começar o problema aqui, a primeira coisa que devemos fazer é simplificar esse circuito.
Temos duas resistências em paralelo, de modo que a resistência equivalente será:
Da mesma forma, temos dois capacitores em paralelo, de forma que a capacitância equivalente será:
Assim, o circuito, que antes tinha uma cara escrota, agora ainda tem uma cara ainda escrota, mas um pouco melhor...
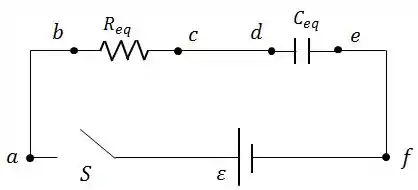
Passo 2
Isso agora nada mais é do que um circuito em série.
Quando o capacitor está inicialmente descarregado, a equação que determina o seu carregamento, é dada por:
Onde o produto é chamado de constante de tempo capacitiva.
Logo:
Passo 3
determine a corrente que atravessa a bateria em função do tempo após o fechamento da chave ;
No passo anterior falamos um pouco de como a carga varia em função do tempo durante o carregamento, certo?
Então, se queremos descobrir a corrente, a única coisa que temos que fazer aqui é derivar a expressão:
Logo:
Substituindo aqui a expressões de e :
Passo 4
determine a entre os ponto e em função do tempo;
Como as resistências e estão em paralelo:
Entretanto, a soma das duas correntes deve ser sempre igual a , logo:
Agora ficou mais tranquilo pro nosso lado:
Substituindo a expressão de :
Passo 5
com fechada por um longo tempo, quais são as cargas nos capacitores e .
Quando , o capacitor atinge a sua carga máxima e a corrente para de circular por ele.
Como vimos antes, a carga do capacitor varia em função do tempo de acordo com a função:
Quando o capacitor atinge a sua carga máxima, diferença de potencial entre os seus terminais é igual a .
Logo, depois de um tempo muito longo, os dois capacitores e estarão completamente carregados e a diferença de potencial entre os terminais de cada um deve ser igual a .
Resposta