Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Circuito RC

Ver Teoria
Exercício 40123456789101112131415161718192021222324252627282930313233343536373839414243444546474849505152535455565758596061626364656667686970717273747576777879808182

Enunciado

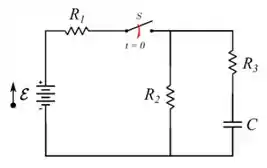
No circuito da figura abaixo a bateria é ideal e possui uma f.e.m. ε   V , o capacitor possui uma capacitância C   F , e os resistores possuem resistências   R 1 , R 2 e R 3 , todas em Ω .

a) Com o capacitor C totalmente descarregado, a chave S é fechada bruscamente no instante   t = 0   s . Determine para o instante t = 0   s , a corrente i 1 no resistor R 1 , a corrente i 2   no resistor R 2   e a corrente i 3 no resistor R 3 .

b) Após passado muito tempo, i.e., após ter passado várias constantes de tempo do circuito, determine a corrente i 1 no resistor R 1 , a corrente i 2 no resistor R 2 e a corrente i 3 no resistor R 3 .

c) Determine a diferença de potencial V 2 no resistor R 2 em t   =   0   s e após muito tempo de fechada a chave, i.e., após ter passado várias constantes de tempo do circuito.

Passo 1

a) O capacitor está descarregado e logo atua como um curto circuito.

No exato instante em que a chave é fechada ( t = 0 ) a corrente que passa pelo circuito vai ser a corrente normal da Lei de Ohm, ou seja

I = ε R e q

Vamos calcular a resistência equivalente do circuito lembrando que R 1 está em série com R 2   e R 3 , que estão em paralelo entre si

R e q = R 1 + R 2 R 3 R 2 + R 3

Ou seja, a corrente total que passa pelo circuito no instante t = 0   s vai ser

I = ε R 1 + R 2 R 3 R 2 + R 3

Essa corrente é a que passa pelo resistor 1, então:

I 1 = ε R 1 + R 2 R 3 R 2 + R 3

I 1 = ε ( R 2 + R 3 ) R 1 R 2 + R 1 R 3 + R 2 R 3   A

Aí a corrente vai se dividir para passar nos resistores 1 e 2, que estão em paralelo. Mas, sabemos que, em paralelo, ambos têm a mesma tensão. Vamos lá.

I 2 = V 2 R 2

E

I 3 = V 2 R 3

E qual é o valor dessa tensão V2?

Bom, vai ser o valor total fornecido ao sistema ( ε ) menos o que foi utilizado ali no resistor 1, então:

V 2 = ε - R 1 I 1

Vamos substituir o valor de I 1 :

V 2 = ε - R 1 ε R 2 + R 3 R 1 R 2 + R 1 R 3 + R 2 R 3

Arrumando isso:

V 2 = ε R 2 R 3 R 1 R 2 + R 1 R 3 + R 2 R 3   V

Show! Vamos voltar e substituir lá na equação para acharmos as correntes i2 e i3.

I 2 = V 2 R 2

I 2 = ε R 2 R 3 R 1 R 2 + R 1 R 3 + R 2 R 3   R 2

I 2 = ε R 3 R 1 R 2 + R 1 R 3 + R 2 R 3   A

E

I 3 = ε R 2 R 3 R 1 R 2 + R 1 R 3 + R 2 R 3   R 3

I 3 = ε R 2 R 1 R 2 + R 1 R 3 + R 2 R 3   A

Passo 2

b) Depois de passado muito tempo, o capacitor já vai estar carregado certo? Ok, agora vamos lembrar que um capacitor carregado se comporta como um circuito aberto!! Então, depois de passado todo esse tempo, a corrente não irá mais passar pela malha de C , ela vai passar apenas por R 1 e R 2 , logo, a corrente total vai depender apenas desses resistores e vai ser dada por

I = ε R 1 + R 2

Nesse caso

I 1 = ε R 1 + R 2

I 2 = ε R 1 + R 2

I 3 = 0

Passo 3

c) Já vimos que depois de muito tempo o capacitor se comporta como um curto circuito, então a corrente não passa por R3. Assim:

ε = R 1 + R 2 I

Portanto, a corrente é:

I = ε R 1 + R 2

E a tensão V2 é:

V 2 = ε - R 1 I

V 2 = ε - R 1 ε R 1 + R 2

V 2 = ε R 2 R 1 + R 2   V

Resposta

  1. I 1 = ε ( R 2 + R 3 ) R 1 R 2 + R 1 R 3 + R 2 R 3   A

    2. I 2 = ε R 3 R 1 R 2 + R 1 R 3 + R 2 R 3   A

    I 3 = ε R 2 R 1 R 2 + R 1 R 3 + R 2 R 3   A

  2. I 1 = ε R 1 + R 2

    3. I 2 = ε R 1 + R 2

    I 3 = 0

  3. V 2 = ε R 2 R 1 + R 2   V

Exercícios de Livros Relacionados

O capacitor C da Figura 25-49 está inicialmente descarregado. Logo após o interruptor S ser fechado, (a) a tensão em C é igual a E, (b) a tensão em R é E. (c) a corrente no circuito é zero, (d) ambas
O circuito mostrado na figura abaixo é uma ponte de Wheatstone e o resistor variável está sendo usado como um potenciômetro de fio deslizante. A resistência R 0 é conhecida. Esta “ponte” PE usada para
Mostre que a Equação d Q d t = ℇ C - Q R C ℇ pode ser reescrita como d Q ℇ C - Q = d t R C ℇ . Integre esta equação para derivar a solução dada pela Equação Q f ( 1 - e - t / R C ) .
No circuito mostrado na figura abaixo, o capacitor tem capacitância de 2.50 μ F e o resistor tem resistência de 0.500M Ω . Antes de a chave ser fechada, a queda de potencial no capacitor é 12.0V , com
A Fig. 27-67 mostra dois circuitos com um capacitar carregado que pode ser descarregado através de um resistor quando uma chave é fechada. Na Fig. 27-67a, R 1 = 20,0 Ω e C 1 = 5,00 μ F . Na Fig. 27-67