Unicamp - Física 3 – P2 2018.1 - DIURNO - 7
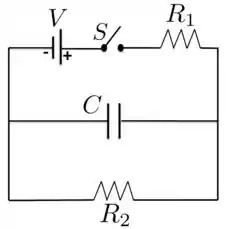
No circuito da figura, a chave S é fechada em . Qual é a carga no capacitor quando ?
- ;
- ;
- ;
- ;
- .
Passo 1
No tempo , o capacitor vai estar totalmente carregado e não vai mais passar corrente por ele. A corrente nesse instante vai passar apenas nos resistores , e na fonte .
Nesse tempo muito grande, a carga total no capacitor vai ser máxima e terá o valor dado por . Então, precisamos encontrar a ddp para .
Para isso, vamos encontrar a corrente que passa nos resistores em série e e fazer , já que o resistor está em paralelo com o capacitor e, por isso, tem a mesma ddp.
Passo 2
A corrente para vai ser:
Então, a ddp no capacitor será:
Com isso, a carga máxima do capacitor será:
Resposta
Letra c.
Exercícios de Livros Relacionados
O capacitor C da Figura 25-49 está inicialmente descarregado. Logo após o interruptor S ser fechado, (a) a tensão em C é igual a E, (b) a tensão em R é E. (c) a corrente no circuito é zero, (d) ambas
O circuito mostrado na figura abaixo é uma ponte de Wheatstone e o resistor variável está sendo usado como um potenciômetro de fio deslizante. A resistência R 0 é conhecida. Esta “ponte” PE usada para
Mostre que a Equação d Q d t = ℇ C - Q R C ℇ pode ser reescrita como d Q ℇ C - Q = d t R C ℇ . Integre esta equação para derivar a solução dada pela Equação Q f ( 1 - e - t / R C ) .
No circuito mostrado na figura abaixo, o capacitor tem capacitância de 2.50 μ F e o resistor tem resistência de 0.500M Ω . Antes de a chave ser fechada, a queda de potencial no capacitor é 12.0V , com
A Fig. 27-67 mostra dois circuitos com um capacitar carregado que pode ser descarregado através de um resistor quando uma chave é fechada. Na Fig. 27-67a, R 1 = 20,0 Ω e C 1 = 5,00 μ F . Na Fig. 27-67