No circuito mostrado na figura abaixo, a chave é fechada no instante . A carga no capacitor nesse instante é . Considere , , , e .
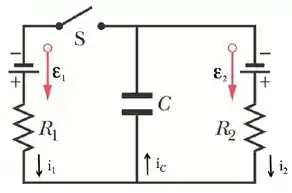
Para tal situação, calcule:
(a) As correntes , e no instante .
(b) As correntes , e para .
(c) A carga no capacitor quando o mesmo está totalmente carregado.
Passo 1
No instante , o capacitor não está carregado e, portanto, não há diferença de potencial entre os seus terminais. Ou seja, ele se comporta como um curto, como na figura abaixo.
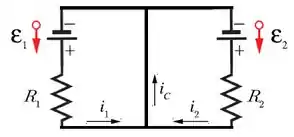
Passo 2
Agora, aplicamos as leis de Kirchhoff para encontrar as expressões abaixo:
- .
- .
- .
Passo 3
Para , o capacitor está completamente carregado e já não passa mais corrente por ele. Ou seja, ele se comporta como um circuito aberto, como na figura abaixo.
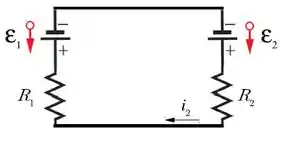
Passo 4
Nesse caso, e . Temos:
Passo 5
A diferen��a de potencial sobre o capacitor é dada por:
A carga será, portanto:
Resposta
(a) No instante , , e .
(b) Para , , e .
(c) A carga no capacitor quando este está totalmente carregado é dada por: