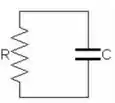
14 - Um capacitor de capacitância e, inicialmente, totalmente carregado com carga , é descarregado através de um resistor de resistência através de fios ideais (Veja a figura ao lado). O campo magnético muito próximo do fio inferior (ou seja, a uma distância muito pequena do fio quando comparada ao seu comprimento) decairá a metade após:
Passo 1
Pois bem! Muito próximo do fio de baixo podemos considerar o fio como infinito, e o campo magnético de um fio infinito é:
Portanto o campo é diretamente proporcional a corrente. Se a corrente cair pela metade, então o campo também cairá! Então temos que encontrar o tempo que a corrente caia pela metade!
Passo 2
Temos uma equação para a descarga do capacitor e que sim... Envolve o tempo:
é a carga inicialmente no capacitor e é a carga com o passar do tempo durante a descarga.
Ora, sabemos que a corrente nada mais é que a variação de carga com o tempo:
Então, derivando...
Substituindo por onde é a corrente de descarga do capacitor...
A corrente inicial (assim que conectar o resistor no ), será de...
Como queremos a corrente que seja a metade da corrente inicial...
Substituindo ...
Agora é só simplificar!
Passo 3
Cancelando os termos iguais dos dois lados e aplicando ...
Como é () e é ()...
Ou . Letra A.
Resposta
Letra A.