No circuito abaixo, a bateria de é ideal e o capacitor encontra-se inicialmente descarregado.
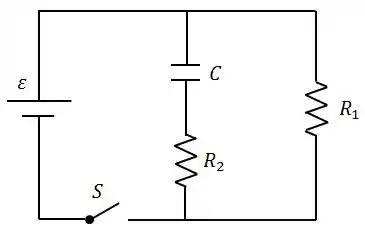
Após ligar a chave , em , calcule:
A corrente que passa pelo resistor ;
A corrente que passa pela chave , imediatamente após ser ligada ;
A carga do capacitor em função do tempo;
A corrente através de em função do tempo;
Passo 1
A corrente que passa pelo resistor ;
A corrente em será dada por:
Passo 2
A corrente que passa pela chave , imediatamente após ser ligada ;
A corrente que passa pela chave será a soma das correntes que passam por e por , logo:
No instante inicial o capacitor funciona como curto circuito, então é como se ele não estivesse no circuito. Sendo assim, a corrente em será dada por:
Assim, a corrente que passa pela chave será:
Passo 3
A carga do capacitor em função do tempo;
Aplicando a lei das malhas na malha que contém , e , teremos:
Onde , logo:
Resolvendo essa equação diferencial, teremos, para o carregamento do capacitor:
Se você não lembrava essa de cabeça, relaxa, no próximo passo vamos fazer isso devagar. Se você se garantir em lembrar a fórmula pode ir direto pro passo 5.
Passo 4
Vamos começar reorganizando esse cara:
Agora podemos separar as variáveis:
Agora basta integrar dos dois lados:
Finalmente:
Passo 5
A corrente através de em função do tempo;
A corrente através de é dada por:
Resposta