UFF - Física 2 – P2 2018.1 - 20
Na figura abaixo temos um circuito formado por um resistor, um capacitor e uma bateria ideal. Inicialmente, o capacitor se encontra descarregado. Se a chave for ligada, quanto tempo, em unidade de , levará para o capacitor atingir da sua carga máxima?
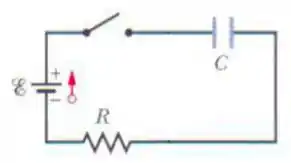
Passo 1
Aqui, precisamos nos lembrar que a carga desse capacitor, inicialmente descarregado, aumenta com o tempo de acordo com a expressão:
Quando o tempo for muito grande, ou seja, no instante , o capacitor estará totalmente carregado. Por isso, de acordo com a equação acima, em a carga total do capacitor será
Passo 2
Agora, vamos dizer que no tempo , a carga do capacitor será , ou seja, da carga total dele. Substituindo isso em
Mexendo um pouco mais nessa expressão, teremos:
Aplicando o ln dos dois lados dessa expressão:
Nesse instante de tempo , a carga do capacitor será de .
Resposta
Letra a.