Um resistor de e um capacitor estão ligados em série, e então uma diferença de potencial de é repentinamente aplicada entre as extremidades deles.
A diferença de potencial entre as extremidades do capacitor aumenta para em .
- Calcule a constante de tempo do circuito;
- Determine a capacitância do capacitor;
Passo 1
O circuito tem mais ou menos essa cara aqui:
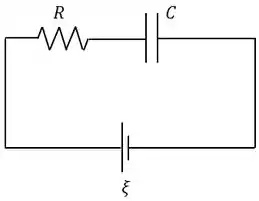
Trata-se de um circuito RC, nele a carga do capacitor, a corrente e d.d.p. do capacitor variam de acordo com as equações:
O circuito RC possui uma grandeza chamada constante de tempo, dada por:
Passo 2
- Calcule a constante de tempo do circuito;
- Determine a capacitância do capacitor;
O problema diz que a diferença de potencial entre as extremidades do capacitor aumenta para em .
Então vamos usar esse dado na equação:
Onde:
;
;
;
Vamos ver no que vai dar:
Passo 3
Conforme eu disse no Passo 1:
Logo:
Agora ficou fácil, né?
;
;
Vambora!
Resposta
- ;
Exercícios de Livros Relacionados
O capacitor C da Figura 25-49 está inicialmente descarregado. Logo após o interruptor S ser fechado, (a) a tensão em C é igual a E, (b) a tensão em R é E. (c) a corrente no circuito é zero, (d) ambas
O circuito mostrado na figura abaixo é uma ponte de Wheatstone e o resistor variável está sendo usado como um potenciômetro de fio deslizante. A resistência R 0 é conhecida. Esta “ponte” PE usada para
Mostre que a Equação d Q d t = ℇ C - Q R C ℇ pode ser reescrita como d Q ℇ C - Q = d t R C ℇ . Integre esta equação para derivar a solução dada pela Equação Q f ( 1 - e - t / R C ) .
No circuito mostrado na figura abaixo, o capacitor tem capacitância de 2.50 μ F e o resistor tem resistência de 0.500M Ω . Antes de a chave ser fechada, a queda de potencial no capacitor é 12.0V , com
A Fig. 27-67 mostra dois circuitos com um capacitar carregado que pode ser descarregado através de um resistor quando uma chave é fechada. Na Fig. 27-67a, R 1 = 20,0 Ω e C 1 = 5,00 μ F . Na Fig. 27-67