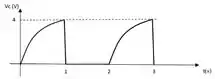
Considere o circuito da Figura 1, onde e S é uma chave que alterna entre as posições 1 e 2 de forma cíclica, de tal forma que a permanência em cada posição tem a duração de 1 segundo.
- Desenhe o gráfico em escala da variação da . no capacitor com dois ciclos da chave S, indicando nos eixos os valores numéricos importantes. NOTA: considere .
- Determine para que a em no inicio da fase seja igual a .
- Com o valor de calcule a corrente fornecida pela bateria no inicio da fase .
-
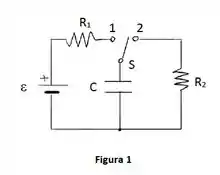
1 e o indutor na figura fossem plenamente energizados nos respectivos circuitos e depois conectados diretamente entre si, formando um circuito , qual seria a frequência angular de oscilação e a amplitude da voltagem do capacitor, após o sistema entrar em oscilação estável?
Considere agora o circuito da Figura 2, onde , o indutor está inicialmente sem energia e ocorrem as seguintes fases sucessivas:
- Fase 1: chave S na posição 1 durante longo tempo;
- Fase 2: chave S na posição 2 durante longo tempo.
Passo 1
Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
Letra (a):
Quando estamos na posição temos que a tensão é dada por:
Aqui temos que:
Agora é só substituir:
Na posição temos:
Nessa posição temos:
Daí a ddp fica:
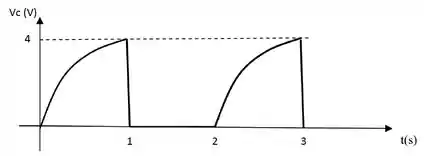
Então agora podemos fazer o gráfico. De até temos um aumento na ddp, indo de até , e depois entre os instantes e temos que a ddp é nula. A partir de temos uma repetição, com o aumento da ddp até o instante , daí novamente uma queda abrupta (por causa do fator exponencial), e entre e nula novamente. O gráfico da tensão pelo tempo fica mais ou menos assim:
Passo 2
Letra (b):
No inicio da fase temos , e resolvendo para a corrente:
Daí temos que é o valor da corrente no final da fase , que é quando a gente chama que o indutor está como um curto, agora ficou tranquilo achar a resistência , já que a ddp ali é :
Tranquilo? Vamos para o terceiro item?
Passo 3
Letra (c):
Com o indutor aberto, isso significa que temos um circuito bem simples, com uma bateria e duas resistências em série. Sabemos que a resistência total nesse caso é a soma das resistências, então a ddp é dividida entre elas:
Beleza? Vamos para o último item dessa questão?
Passo 4
Letra (d):
A frequência de oscilação é:
E a amplitude de voltagem a gente pode achar através da conservação de energia.
Quando os dois componentes estão plenamente energizados, então em termos de energia total temos:
Os valores de e vou resgatar dos itens anteriores e substituir tudo ali em cima:
E para uma osculação estável temos:
E assim conseguimos determinar :
Beleza?
Pronto pra próxima questão? =)
Resposta