Considere o sistema de equações lineares abaixo. Encontre a(s) condição(ões) sobre a, b e c para que o sistema seja possível. E, neste caso, diga qual o grau de liberdade do sistema.
Passo 1
Vamos transformar esse sistema em uma matriz aumentada e então escalonar para ficar fácil de ver as relações entre a, b e c.
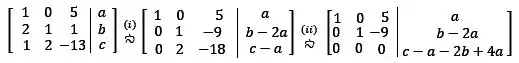
Passo (i): e
Passo (ii):
Passo 2
Agora note que na última linha temos todos os coeficientes iguais a zero.
Para que isso seja possível, o lado direito também deve ser zero.
Então:
com a e b números reais.
Portanto essa é a condição para que o sistema seja possível!
Passo 3
O grau de liberdade de um sistema é igual ao número de variáveis livres.
Olhando para a matriz que escalonamos no passo 1, podemos reescrever as duas primeiras linhas como duas equações da forma:
Isolando o x na primeira linha, obtemos:
Isolando o y na segunda:
Como a e b são números reais, se temos um valor para z, conseguimos achar valores para x e y a partir das equações que acabamos de obter.
O z então é uma variável livre, enquanto x e y são variáveis dependentes.
Logo, o grau de liberdade do sistema é 1.
Resposta
1 grau de liberdade