UnB; Introdução à Álgebra Linear; 1ª Lista de Exercícios – Turma E; Exercício 10
10) O sistema seguinte não tem solução para quais valores de ? Exatamente uma solução? Infinitas soluções?
Passo 1
Oi pessoal, como vão?? Me contaram aqui que vocês estão suuuper animados com essa resolução, felizes pra caramba, como nunca estiveram!!
Não quero saber de desânimo!! Bora transformar ela em algo legal e mais atrativo? hahahaha a gente consegue, acreditem!! Bora lá!!
O enunciado pergunta para quais valores de o sistema não tem soluções.
Tá, mas como descobrimos isso?
Antes de tudo, o meio mais fácil de trabalharmos com o sistema que o enunciado deu é transformando-o em matriz aumentada!
Então, vamos ter o seguinte:
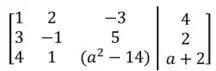
Tá, mas como isso me ajuda aqui?
A matriz do jeito que está ali em cima não vai nos ajudar muito mesmo, e pra deixarmos ela funcional, devemos primeiramente escaloná-la, de modo a deixar os números abaixo da diagonal principal igual a zero!
Vamos lá então!
Passo 2
Para deixar a matriz acima com abaixo da diagonal principal vamos realizar algumas operações de linhas! Pra isso vamos chamar as linhas e de e , respectivamente.
Começaremos com: :
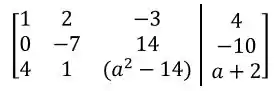
Agora, faremos :
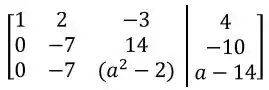
Então, multiplicaremos por :
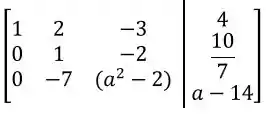
Por fim, faremos :
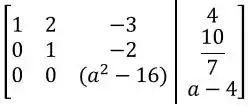
Prontinho! Encontramos um formato simplificado por escalonamento da nossa matriz aumentada.
Mas e agora? O que eu faço com isso?
Calma que é mais simples do que parece!
Passo 3
Para que o sistema não possua soluções, a última equação deve ser impossível. Isso acontece se for igual a zero e não.
Vamos então analisar a última equação, lembrando que a matriz aumentada tem apenas os coeficientes no lado esquerdo. Assim, após o escalonamento, o que temos, na realidade, pela última equação é que:
Não queremos que o sistema tenha solução, então não pode ter solução. Isso vai acontecer quando??
É só lembrar do mandamento: Não dividirás por zero!!!
Portanto, para que não haja solução devemos ter:
É isso então?? Opaaa. Tem um detalhe, se tivermos algo do tipo é uma indeterminação matemática, é como se o sistema tivesse infinitas soluções. Então, devemos ter o numerador diferente de zero. Logo:
Daí, fazendo intersecção desses dois casos, temos que o sistema é impossível apenas se:
Eaí, entendeu direitinho? 😊
Sendo assim:
Assim, como chegamos a conclusão que !
Então, o sistema não apresenta soluções quando !
Uhul!! Terminamos pessoal! Mais simples do que parece, não é mesmo?
Bora lá pra próxima então?