Exercícios Resolvidos de Direção de Crescimento Mais Rápido da Derivada Direcional
Ver TeoriaEnunciado
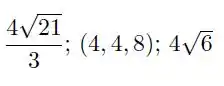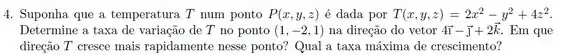
Passo 1
Calcular módulo do vetor :
Passo 2
Calcular vetor gradiente:
Substituindo no ponto :
Passo 3
Calcular derivada direcional:
Passo 4
A direção que a função cresce mais rapidamente no ponto é a direção do vetor gradiente, ou seja, é a direção
Que já calculamos no passo 2.
Passo 5
E a taxa de crescimento máximo da função é dada pelo módulo do vetor gradiente:
Resposta
Exercícios de Livros Relacionados
Determine a taxa de variação máxima de f no ponto dado e a direção em que isso ocorre. f x , y = sin x y ,1,0
Perto de uma boia, a profundidade de um lago com coordenadas x , y é z = 200 + 0.02 x 2 - 0.001 y 3 , onde x ,y e z são medido em metros. Um pescador em um pequeno barco começa no ponto 80,60 e se mov
Mostrar que uma função diferenciável f diminui mais rapidamente em x na direção oposta ao vetor gradiente, ou seja, na direção de - ∇ f x Use o resultado da parte (a) para encontrar a direção qual a f
Determine a taxa de variação máxima de f no ponto dado e a direção em que isso ocorre. f x ,y ,z = x 2 + y 2 + z 2 , ( 3 ,6 ,- 2 )
Determine as direções em que a derivada direcional de f x , y = y e - x y no ponto 0 ,2 tem valor 1 .