Exercícios Resolvidos de Direção de Crescimento Mais Rápido da Derivada Direcional
Ver TeoriaEnunciado
Derivadas Direcionais
Considere a função Para que a derivada direcional seja máxima, o ângulo que o vetor deve formar com o eixo é:
(a)
(b)
(c)
(d)
(e)
Passo 1
O crescimento é máximo no sentido do vetor gradiente. Então para que seja máxima o vetor tem que estar na mesma direção e sentido de . Então vamos calcular esse gradiente! Pela regra do produto:
Também temos:
Logo:
Passo 2
Portanto, o vetor tem que ser paralelo ao vetor . Então os dois vetores têm que fazer o mesmo ângulo com o eixo ! Mas o vetor é paralelo ao eixo :
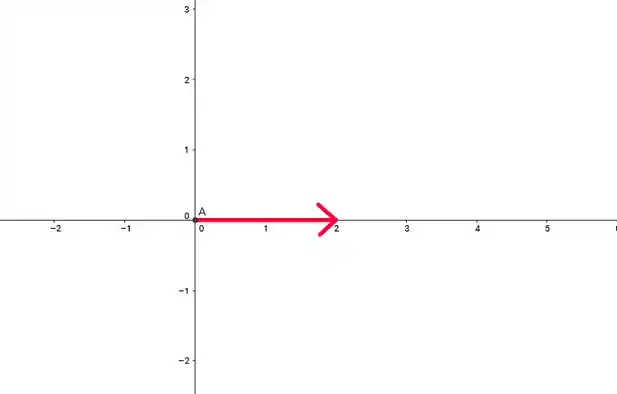
Ou seja, o ângulo entre o vetor e o eixo é . Então o vetor também vai ter que formar um ângulo de com o eixo .
Resposta
Alternativa (e)
Exercícios de Livros Relacionados
Determine a taxa de variação máxima de f no ponto dado e a direção em que isso ocorre. f x , y = sin x y ,1,0
Perto de uma boia, a profundidade de um lago com coordenadas x , y é z = 200 + 0.02 x 2 - 0.001 y 3 , onde x ,y e z são medido em metros. Um pescador em um pequeno barco começa no ponto 80,60 e se mov
Mostrar que uma função diferenciável f diminui mais rapidamente em x na direção oposta ao vetor gradiente, ou seja, na direção de - ∇ f x Use o resultado da parte (a) para encontrar a direção qual a f
Determine a taxa de variação máxima de f no ponto dado e a direção em que isso ocorre. f x ,y ,z = x 2 + y 2 + z 2 , ( 3 ,6 ,- 2 )
Determine as direções em que a derivada direcional de f x , y = y e - x y no ponto 0 ,2 tem valor 1 .