Você está no ponto em uma colina com a forma dada pelo gráfico de , com , e dados em metros.

a) Em que direção, no plano , você deveria sair para fazer a subida mais íngreme?

b) Qual a taxa de variação nessa direção?

c) A que ângulo, em relação à horizontal, você estará subindo inicialmente?

b) Qual o valor da taxa nessa direção que encontramos? É a norma do vetor! Então, partiu encontrar esse módulo! Lembra como fazemos isso? Pegamos a raiz quadrada das coordenadas ao quadrado somadas:

Simples assim! Nossa taxa de variação é de

Agora, temos que saber qual é o ângulo que o vetor gradiente faz com a horizontal. Para isso, precisamos imaginar o seguinte: Estamos num ponto da nossa montanha, e sabemos qual é a direção no plano que devemos seguir. Mas, se seguíssemos nessa direção, estaríamos furando a montanha ou pulando para fora dela! Para visualizar melhor essa questão, é esse aqui o problema:

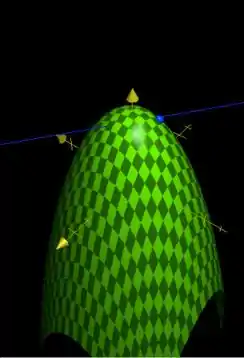
Esse ponto azul é o lugar onde estamos, e a reta é a que tem direção no plano , que levamos até o nosso ponto.

Ou seja, já temos duas componentes da nossa direção: . Precisamos, agora, saber qual é a componente do vetor diretor (para que, dando o próximo passo, ainda estejamos na superfície da montanha!). Então, que vetor é esse? É um vetor tangente à superfície da montanha! E daí, como faremos pra descobri-lo? Acho que a maneira mais fácil é pensar que ele pertence ao plano tangente à montanha neste ponto que estamos!

Beleza, então, nossa estratégia será: -Encontremos o plano tangente; -Substituir as coordenadas na equação do plano e ver qual é a altura correspondente. - Aí, para saber a inclinação da direção que estamos caminhando, basta dividir a altura encontrada pela norma do vetor no plano , e teremos a tangente do ângulo!

Para encontrar o plano tangente, precisamos do gradiente de , sabendo que

Então, , pois a derivada é sempre ! Como já calculamos e (que são as tão comentadas coordenadas da direção de maior crescimento), fica:

Como já temos o ponto de tangência, que é o próprio que estamos, só precisamos jogar o vetor gradiente e esse ponto na equação do plano:

Desenvolvendo...

E aí está a equação do plano tangente!

Olha como ele casou certinho com o nosso desenho:

Estamos quase! Segura aí que a resposta está vindo! O que precisamos fazer? Já temos nosso plano tangente, já temos a direção no plano ... E agora? Agora só precisamos pegar um ponto no plano cuja projeção esteja sobre a reta de direção ! Sim, pois essa é a direção no plano que nos dá o maior crescimento! Por exemplo, só pra não ter essas vírgulas todas, se colocamos no plano e , temos :

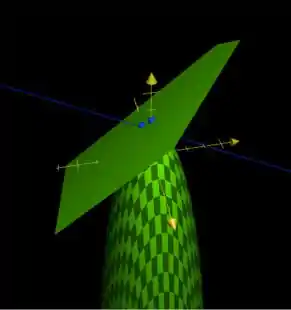
Está vendo essa outra bolinha que apareceu? É o ponto ! Se ligarmos ela ao ponto que estamos, que é a bolinha de baixo, teremos o ângulo com a horizontal ;) Também serviria se escolhêssemos , ou qualquer outro múltiplo do vetor , entendeu? Só iria mudas a altura , mas a proporção e o ângulo de inclinação, não!

Partiu encontrar esse ângulo! Basta encontrar a tangente dessa inclinação, que será a diferença de altura (diferença no eixo ) dividida pela distância no plano das coordenadas dos dois pontos.

84850000001-3 24620089999-7 99599999911-0 33610832749-3

Para a diferença entre as alturas, temos:

Ela é a diferença entre a terceira coordenada do ponto , o mais alto, menos a terceira coordenada do ponto , mais baixo, sobre o paraboloide.

Para a diferença entre as distâncias no plano , precisamos, primeiro ver a distância à origem, percorrida no plano , para cada ponto. Para o primeiro, teremos . Para a distância à origem no plano do segundo ponto temos .

Assim, a diferença será

E, por fim, fazendo a tangente, temos essa coisa feia, dividindo um valor pelo outro:

Fazendo numa calculadora, temos , aproximadamente... Parece realmente bater com a realidade!