Considere a função

Determine:

1. A direção ou direções em que a derivada direcional de no ponto é igual a .
2. A direção ou direções em que a derivada direcional é máxima e encontre esse valor máximo. Use o mesmo ponto do item .

Observação: as direções são dadas por vetores unitários.

Vamos lá.

No ponto :

Substituindo na fórmula da derivada direcional:

Fazendo esse produto escalar, temos

Como o vetor deve ser um vetor unitário, temos:

Ok, mas parece que isso não nos levou a nada, não é mesmo? Porque a gente ainda não sabe quem é a componente , então a gente ainda não sabe o vetor....

Pois então vamos imaginar como seria o vetor no plano:

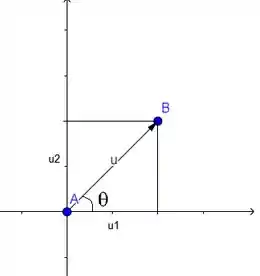
Por essa figura, podemos tirar que

Tranquilo?

Mas, de novo, considerando que o vetor é um vetor unitário, teremos que , que representa o módulo do vetor , vai valer um, assim

OPAA, mas a gente tinha achado no passo 2 que

Então

E o ângulo cujo cosseno vale é

Substituindo esses resultados em

Temos

E

Dessa forma, temos os vetores

E

Que representam as direções em que a derivada direcional de no ponto é igual a .

A direção em que a derivada direcional é máxima é dada pela direção do vetor gradiente.

Assim, o vetor que procuramos aqui é o vetor

Observe que ele já tem módulo 1. Assim, a gente nem precisa dividir ele pelo módulo!

O valor máximo da derivada direcional é dado pelo módulo do vetor gradiente. E, nesse caso, já vimos que nosso vetor gradiente tem módulo 1, assim: