Um anel de raio , com uma carga uniformemente distribuída, é colocado no plano , com seu centro na origem de um sistema de coordenadas cartesianas. Calcule o potencial devido ao anel em um ponto qualquer qualquer do eixo z.
Passo 1
Para calcularmos o potencial no ponto , vamos usar
Mas ainda precisamos saber ose , depende do anel, porém, vemos que é constante:
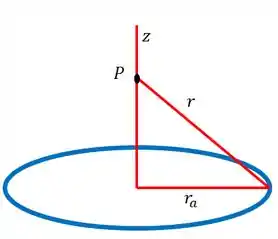
Por isso temos que
Como é constante podemos colocar para fora da integral e por último, podemos substituir
Lembrando que o enunciado já nos disse que a carga no anel é , então
Assim, chegamos que o potencial no ponto é
Resposta
Exercícios de Livros Relacionados
Considere uma carga pontual q = 1,0 μC, o ponto A a uma distância d 1 = 2,0m de q e o ponto B a uma distância d 2 = 1,0m de q. (a) Se A e B estão diametralmente opostos, como na figura da esquerda aba
A figura (a) mostra duas partículas carregadas. A partícula 1, de carga q 1 , é mantida fixa no lugar a uma distância d da origem. A partícula 2, de carga q 2 , pode ser deslocada ao longo do eixo x.
Na figura (a), uma partícula de carga +e está inicialmente no ponto z = 20 nm do eixo de um dipolo elétrico, do lado positivo do dipolo. (A origem do eixo zé o centro do dipolo.) A partícula é desloca
A figura (a) mostra três partículas no eixo x. A partícula 1 (com uma carga de +5,0 μC) e a partícula 2 (com uma carga de +3,0 μC) são mantidas fixas no lugar, separadas por uma distância d = 4,0 cm.
Um pósitron (carga + e , massa igual à do elétron) está se movendo com uma velocidade de 1 , 0 · 10 7m / s no sentido positivo do eixo x quando, em x = 0 , encontra um campo elétrico paralelo ao eixo