Considere um disco de raio cuja densidade de carga é .
Determine:
O potencial elétrico no ponto , localizado a uma distância acima do centro do disco, conforme a figura ao lado.
O campo elétrico no ponto .
O valor do campo elétrico no limite .
O valor do potencial elétrico no limite .
Passo 1
O potencial elétrico no ponto , localizado a uma distância acima do centro do disco, conforme a figura ao lado.
A ideia inicial é dividir esse disco em vários anéis concêntricos, cada um com carga . Vamos começar escrevendo o potencial elétrico gerado por cada um desses anéis no ponto .
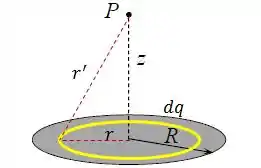
Onde e . Logo:
Onde, tratando-se de um anel, :
Substituindo do enunciado
Assim, o potencial elétrico resultante será:
Agora o problema é basicamente cálculo.
Passo 2
Vamos resolver essa integral com uma substituição simples, beleza?
O numerador dentro da integral fica
E os limites de integração serão
Logo:
Passo 3
O campo elétrico no ponto .
O campo elétrico pode ser definido através do potencial elétrico pela relação dada por:
Como o campo depende exclusivamente de :
Um detalhe mega importante é a derivada de ! A função módulo sempre retorna um valor positivo, mas a sua derivada não! Como para , é decrescente, logo . Assim
Dá pra juntar os dois primeiros termos
Assim:
Jogando o sinal negativo para dentro dos colchetes, teremos:
Passo 4
O valor do campo elétrico no limite .
Para o primeiro termo será dado por
Assim
Passo 5
O valor do potencial elétrico no limite .
Vamos olhar para o potencial
Pra facilitar a nossa vida vamos trabalhar com , de forma que .
Se fizermos direto vamos ter
O que por um lado é bom que nos diz que o potencial vai pra 0 no infinito mas por outro é ruim por que não nos diz COMO! Pra isso temos que fazer uma expansão assintótica!
Como temos umas raízes o ideal é que possamos escrever cada uma delas na forma
Para podermos usar a expansão binomial (ou série de Taylor) para
Como , o nosso parâmetro de expansão será algo como , que será ! Assim podemos rescrever as raízes
Que, fazendo teremos a seguinte expansão
E
Que, fazendo teremos a seguinte expansão
Substituindo no potencial elétrico teremos
Que deu .... Fazer o que agora??? Temos que pegar mais um termo na expansão :o
Não precisa fazer toda a conta de novo já que a gente sabe que os dois primeiros termos das expansões se anulam! Assim
Sendo que o cara que nos interessa é o terceiro!
Já a outra raiz
Aí agora sim partindo pro potencial
A gente sabe que só sobrevivem os terceiros termos das expansões das raízes, assim
Agora FINALMENTE!!!
Resposta