Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Potencial Elétrico Gerado por Carga Pontual

Ver Teoria
Exercício 612345789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Sabendo que, na figura, a = 4,0   c m e que o módulo de q vale 3,0   n C , responda:

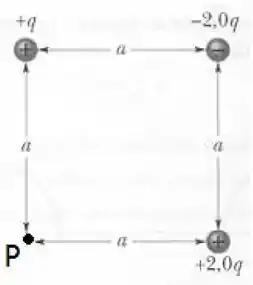
a ) Qual é o valor do potencial elétrico no ponto P ?

b ) Qual é a variação energia potencial elétrica para trazermos uma carga de prova q 0 = 1,0   n C do infinito até o ponto P ?

Passo 1

Para determinar o potencial elétrico em um ponto gerando por um conjunto de cargas puntiformes, podemos utilizar o princípio da superposição, basta calcular o potencial gerado por cada carga separado e depois somar.

A diferença de potencial é dada por:

Δ V = - ∫ E → . d r →

Lembrando que o campo produzido por uma carga puntiforme é:

E = k . q r 2

Substituindo, temos:

Δ V = - k . q ∫ 1 r 2 d r

Δ V = k . q . r - 1 ∞ d

Lembrando que 1 ∞ tende a zero, temos:

V = k . q . d - 1

Onde d será a distância entre o ponto P e a carga analisada, vamos começar a calcular!

Passo 2

Para 2,0 q , que dista d = 4,0   c m de P , temos:

V 2,0 q P = k . q . 4 × 10 - 2 - 1

V 2,0 q P = 9 × 10 9 .   2,0.3,0 × 10 - 9 . 4 × 10 - 2 - 1

V 2,0 q P = 1350   V

Para - 2,0 q , que dista d = 4,0 . 2   c m de P , temos:

V - 2,0 q P = k . - 2,0 q . 4 . 2 × 10 - 2 - 1

V - 2,0 q P = - 9 × 10 9 .   2,0.3,0 × 10 - 9 . 4 2 × 10 - 2 - 1

V 2,0 q P = - 954,6   V

Para q , que dista d = 4,0   c m de P , temos:

V q P = k . q . 4 × 10 - 2 - 1

V q P = 9 × 10 9 . 3,0 × 10 - 9 . 4 × 10 - 2 - 1

V q P = 675   V

Portanto, o potencial no ponto P , será:

V P = V 2,0 q P + V 2,0 q P + V q P

V P = 1350 - 954,6 + 675 = 1070,4   V

Passo 3

b )

Para determinar a energia para trazer uma carga q 0 do infinito até o ponto P , devemos utilizar a seguinte fórmula:

Δ V = Δ U q

V P - V ∞ = Δ U q 0

1070,4 - 0 = Δ U 1,0 × 10 - 9

Δ U = 1,07 × 10 - 6   J

Resposta

a )   V P = 1070,4   V

b )   Δ U = 1,07 × 10 - 6   J

Exercícios de Livros Relacionados

Considere uma carga pontual q = 1,0 μC, o ponto A a uma distância d 1 = 2,0m de q e o ponto B a uma distância d 2 = 1,0m de q. (a) Se A e B estão diametralmente opostos, como na figura da esquerda aba
A figura (a) mostra duas partículas carregadas. A partícula 1, de carga q 1 , é mantida fixa no lugar a uma distância d da origem. A partícula 2, de carga q 2 , pode ser deslocada ao longo do eixo x.
Na figura (a), uma partícula de carga +e está inicialmente no ponto z = 20 nm do eixo de um dipolo elétrico, do lado positivo do dipolo. (A origem do eixo zé o centro do dipolo.) A partícula é desloca
A figura (a) mostra três partículas no eixo x. A partícula 1 (com uma carga de +5,0 μC) e a partícula 2 (com uma carga de +3,0 μC) são mantidas fixas no lugar, separadas por uma distância d = 4,0 cm.
Um pósitron (carga + e , massa igual à do elétron) está se movendo com uma velocidade de 1 , 0 · 10 7m / s no sentido positivo do eixo x quando, em x = 0 , encontra um campo elétrico paralelo ao eixo