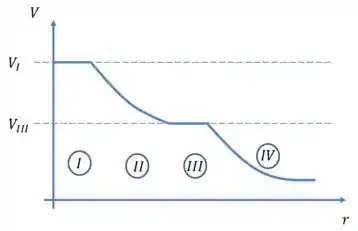
Considere o gráfico que mostra como o potencial eletrostático varia em função da distância radial a partir de um determinado ponto central em cada uma de 4 regiões distintas do espaço. Nas regiões I e III, o potencial é constante, ao passo que, nas regiões II e IV, ele decresce suavemente, como mostra a figura. Podemos afirmar que:
a) A componente radial do campo elétrico é negativa nas regiões I e II
b) A componente radial do campo elétrico é nula nas regiões I e III
c) A componente radial do campo elétrico é negativa nas regiões II e IV
d) A componente radial do campo elétrico é nula nas regiões II e IV
e) A componente radial do campo elétrico é positiva em todas as quatro regiões
Passo 1
Sabemos que:
Portanto, neste caso:
Vamos analisar as partes do gráfico.
Passo 2
Na região I, o potencial é constante e, portanto, o campo elétrico é nulo.
Na região II, o potencial decresce, portanto, o campo elétrico é positivo e pode ou não variar com .
Na região III, o potencial é constante e, portanto, o campo elétrico é nulo
Na região IV, o potencial decresce, portanto, o campo elétrico é positivo e pode ou não variar com .
Passo 3
Analisando as alternativas, temos que a resposta correta é a letra (b)
Resposta
(b)