Dois planos infinitos e , paralelos entre si, de densidades superficiais e , estão localizados respectivamente em e .
Calcule detalhadamente o campo elétrico produzido apenas pelo plano , tanto para como para .
De posse desse resultado, encontre o campo elétrico produzido pelos 2 planos na região .
Determine a diferença de potencial entre o plano e o plano , ou seja, .
Passo 1
Calcule detalhadamente o campo elétrico produzido apenas pelo plano , tanto para como para .
Vamos lá!
Por conta da simetria do problema, por se tratar de um plano infinito, o campo elétrico sempre terá direção perpendicular ao plano e o campo elétrico será constante, independente da coordenada .
Além disso, por conta da simetria do plano, podemos dizer que:
Até aí, beleza, mas como vamos calcular o campo elétrico?
Eu sei que você pensou o mesmo que eu... lei de Gauss.
Como gaussiana, vamos pensar em um cilindro de área transversal , cujo eixo de simetria é perpendicular ao plano infinico .
De acordo com a lei de Gauss, o fluxo elétrico através da gaussiana é dado por:
Passo 2
O fluxo através da gaussiana só pode ocorrer através da face lateral do cilindro ou através das tampas, concorda?
Logo:
Mas se tanto quanto o eixo de simetria da gaussiana são perpendiculares ao plano , logo:
Assim, o fluxo elétrico se dará apenas nas tampas.
Como já dissemos, o campo elétrico é constante, e como a gaussiana possui duas tampas de área , podemos dizer que:
Passo 3
Ok, agora vamos para o outro lado da lei de Gauss, que diz que o fluxo elétrico através da gaussiana é dado por:
A carga interna está relacionada à densidade de carga por:
Substituindo na expressão de , teremos:
Igualando as duas expressões do fluxo elétrico, teremos:
Finalmente:
Como a densidade de carga é negativa:
- :
- :
Passo 4
De posse desse resultado, encontre o campo elétrico produzido pelos 2 planos na região .
O campo elétrico resultante nessa região será:
Se fizermos um desenho desses dois planos
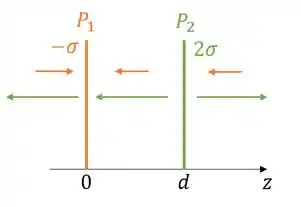
Aqui a gente já vê que o campo elétrico tem que apontar na direção .
Nessa região o campo gerado pelo plano é
E, aplicando o mesmo raciocínio para o plano :
Finalmente:
Passo 5
Determine a diferença de potencial entre o plano e o plano , ou seja, .
No item anterior, concluímos que o campo elétrico na região entre os planos é dado por:
A diferença de potencial está associada ao campo elétrico por:
Onde , logo:
Onde .
Mas como o problema pediu , teremos:
Resposta
(a)
- :
- :
(b)
(b)