Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Potencial Elétrico Gerado por Carga Pontual

Ver Teoria
Exercício 951234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939496979899100

Enunciado

Campos Elétricos e Corpos Carregados, Densidade de Carga, Potencial Elétrico

Uma barra semi-infinita, mostrada na figura ao longo do lado positivo do eixo horizontal x , possui carga positiva homogeneamente distribuída com densidade linear λ .

  1. Determine o vetor campo elétrico num ponto P = ( 0 , y ) sobre o lado positivo do eixo y .
  2. Calcule a diferença de potencial eletrostático Δ V = V B - V A entre os pontos A = 0 , a e B = 0 , b sobre o lado positivo do eixo y , como indicados na figura.

Passo 1

  1. Determine o vetor campo elétrico num ponto P = ( 0 , y ) sobre o lado positivo do eixo y .

    2. Beleza, pra resolver esse tipo de problema, nós vamos pegar uma parte infinitesimal da barra, com carga d q e, a partir dela, chegar à expressão do campo elétrico da barra.

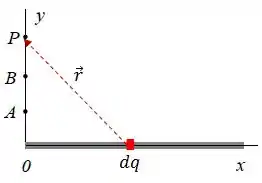
    O campo elétrico gerado pelo elemento de carga d q é dado por:

    d E → = d q 4 π ϵ 0 r 2   r ^

    Onde:

    r ^ = r → r

    Logo:

    d E → = d q 4 π ϵ 0 r 3   r →

    Guarda isso que eu vou te falar agora, ok? Sempre que for resolver esse tipo de problema, você necessariamente vai ter que decompor o vetor de campo elétrico, beleza?

    Então vamos fazer isso no próximo passo.

    Passo 2

    Olhando a figura, podemos escrever o vetor r → = - x i ^ + y j ^ . Consegue ver isso?

    Isso acontece porque o vetor aponta no sentido negativo do eixo x e no sentido positivo do eixo y .

    Continuando...

    Sendo esse o vetor r → , a distância r será:

    r = x 2 + y 2

    Passo 3

    Antes de voltarmos pra fórmula, repara que a carga infinitesimal d q pode ser escrita em função da densidade linear de carga λ .

    d q = λ d x

    O d x apareceu porque a barra está posicionada ao longo do eixo x .

    Agora sim!

    Passo 4

    No passo 1, nós achamos o seguinte:

    d E → = d q 4 π ϵ 0 r 3   r →

    Nos passos 2 e 3, vimos que:

    r → = - x i ^ + y j ^

    r = x 2 + y 2

    d q = λ d x

    Substituindo tudo isso na fórmula, teremos:

    d E → = λ 4 π ϵ 0   - x x 2 + y 2 3 / 2   d x   i ^ + y x 2 + y 2 3 / 2   d x   j ^

    Confere aí! ;)

    Agora é “só” integrar isso tudo! (o que, pra mim, é a parte mais chata)

    Lembrando que x varia entre 0 e + ∞ .

    E → = λ 4 π ϵ 0   - ∫ 0 ∞ x x 2 + y 2 3 / 2   d x   i ^ + y ∫ 0 ∞ 1 x 2 + y 2 3 / 2   d x   j ^

    Bom, aqui não vale muito a pena ficarmos quebrando a cabeça com isso, então vou pelo menos te dizer como começar a resolver o problema, beleza?

    A primeira integral

    ∫ 0 ∞ x x 2 + y 2 3 / 2   d x = 1 x 2 + y 2 1 / 2 0 ∞

    é resolvida com substituição simples, se você chamar u = x 2 + y 2 e d u = 2 x   d x . Lembrando que, já que estamos resolvendo pra x , trataremos y como uma constante.

    A segunda integral

    ∫ 0 ∞ 1 x 2 + y 2 3 / 2   d x = x y 2 x 2 + y 2 1 / 2 0 ∞

    é resolvida por substituição trigonométrica, se você chamar x = y tan ⁡ θ e d x = y sec 2 ⁡ θ   d θ .

    Só vale lembrar que na prova você vai ter que quebrar a cabeça e resolver essas integrais, então é mais fácil quebrar a cabeça agora e saber pra onde ir caso você tenha que resolver uma dessas na prova, beleza?

    Resolvidas as integrais, você vai encontrar:

    E → = λ 4 π ϵ 0 y   - i ^ + j ^

    Passo 5

  2. Calcule a diferença de potencial eletrostático Δ V = V B - V A entre os pontos A = 0 , a e B = 0 , b sobre o lado positivo do eixo y , como indicados na figura.

Por definição, o potencial elétrico pode ser escrito por:

Δ V = - ∫ C   E → ∙ d r →

Portanto, podemos integrar a expressão que encontramos na letra (a) entre os ponto a e b .

Como os pontos a e b estão sobre o eixo y , d r → = d y j ^ . Logo:

Δ V = - λ 4 π ϵ 0 ∫ a b d y y   - i ^ , j ^ ∙ ( 0 , j ^ )

Δ V = - λ 4 π ϵ 0 ∫ a b d y y

Δ V = - λ 4 π ϵ 0 log ⁡ y a b = λ 4 π ϵ 0   log ⁡ ( a ) - log ⁡ b

Δ V = λ 4 π ϵ 0 log ⁡ a b

Resposta

  1. E → = λ 4 π ϵ 0 - i ^ + j ^

Δ V = λ 4 π ϵ 0 log ⁡ a b

Exercícios de Livros Relacionados

Considere uma carga pontual q = 1,0 μC, o ponto A a uma distância d 1 = 2,0m de q e o ponto B a uma distância d 2 = 1,0m de q. (a) Se A e B estão diametralmente opostos, como na figura da esquerda aba
A figura (a) mostra duas partículas carregadas. A partícula 1, de carga q 1 , é mantida fixa no lugar a uma distância d da origem. A partícula 2, de carga q 2 , pode ser deslocada ao longo do eixo x.
Na figura (a), uma partícula de carga +e está inicialmente no ponto z = 20 nm do eixo de um dipolo elétrico, do lado positivo do dipolo. (A origem do eixo zé o centro do dipolo.) A partícula é desloca
A figura (a) mostra três partículas no eixo x. A partícula 1 (com uma carga de +5,0 μC) e a partícula 2 (com uma carga de +3,0 μC) são mantidas fixas no lugar, separadas por uma distância d = 4,0 cm.
Um pósitron (carga + e , massa igual à do elétron) está se movendo com uma velocidade de 1 , 0 · 10 7m / s no sentido positivo do eixo x quando, em x = 0 , encontra um campo elétrico paralelo ao eixo