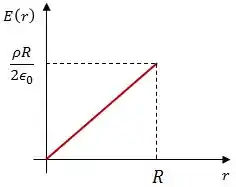
Uma carga elétrica está uniformemente distribuída com densidade volumétrica constante em um volume cilíndrico reto, de comprimento infinito e raio (veja a figura abaixo).

Considere que o potencial elétrico é igual a zero em , onde denota a distância até o eixo de simetria do cilindro maciço.
Nessas condições,
Calcule o módulo do campo elétrico para .
Calcule o potencial elétrico para .
Calcule a diferença de potencial entre o ponto e o ponto .
Faça os gráficos do campo elétrico e do potencial elétrico em função de , para .
Passo 1
Calcule o módulo do campo elétrico para .
Aplicando a Lei de Gauss à simetria cilíndrica, teremos:
Onde é o raio da seção transversal da nossa gaussiana cilíndrica.
Nesse caso, a gaussiana engloba apenas parte do cilindro, logo:
Logo, o campo elétrico será dado por:
Passo 2
Calcule o potencial elétrico para .
O potencial elétrico está relacionado ao campo elétrico pela equação:
Aplicando ao nosso caso, teremos:
Onde . Logo:
Passo 3
Calcule a diferença de potencial entre o ponto e o ponto .
Passo 4
Faça os gráficos do campo elétrico e do potencial elétrico em função de , para .
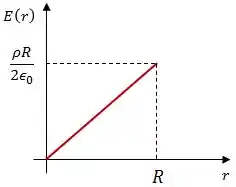
O campo elétrico varia linearmente com o raio, então vai ter essa cara.
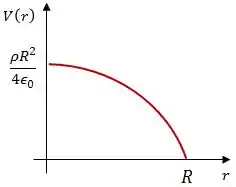
Já o potencial é uma equação de segundo grau, com a concavidade voltada para baixo.
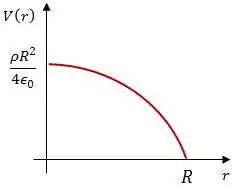
Resposta