Uma carga positiva está localizada no ponto e e uma carga negativa está localizada no ponto e .
- Deduza uma relação para o potencial em qualquer ponto sobre o eixo em função da coordenada .
- Mostre que, quando , o potencial em qualquer ponto sobre a parte positiva do eixo é dado por
- Qual seria a resposta dos itens (b) e (c) se as cargas fossem trocadas de posição, ou seja, se fosse localizada em e em ?
Passo 1
a) A situação que a gente tem aqui está representada na Figura abaixo. Como o potencial depende das cargas e da distância delas até o ponto que está na posição , vamos utilizar as distâncias e indicadas.
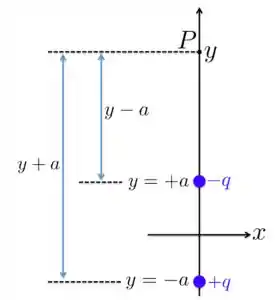
Portanto, o potencial total gerado pelas cargas no ponto é
Quando simplificamos essa expressão, temos o seguinte:
Passo 2
b) Se , temos também que
Com isso, o potencial é simplificado para
Essa expressão dá o potencial gerado pelo dipolo elétrico de módulo no ponto , que está a uma distância .
Passo 3
c) Se a gente troca as cargas de posição, o potencial nessa nova situação é
Simplificando um pouco mais essa expressão,
o que mostra que a inversão das cargas apenas muda o sinal do potencial.
Portanto, para