Densidade de Carga, Campos Elétricos e Corpos Carregados, Potencial Elétrico
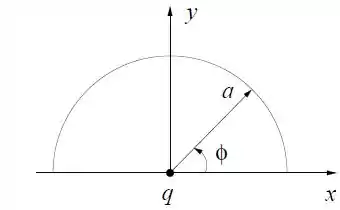
Considere o sistema abaixo, mantido fixo por forças externas, que consiste numa partícula pontual de carga e massa , situada na origem do sistema de coordenadas, e um semi-anel de raio situado no plano e centrado na origem. A densidade linear de carga do semi-anel depende do ângulo de acordo com a seguinte função: , onde é uma constante positiva.
Calcule a carga total do anel;
Calcule o vetor força elétrica que age sobre a carga pontual;
Suponha que o anel é mantido fixo na sua posição e a partícula é liberada a partir do repouso. Qual será o módulo da velocidade da partícula quando ela se encontrar muito longe do anel?
Passo 1
Calcule a carga total do anel;
Por definição, a densidade linear de carga é dada por:
Assim, a carga total do anel será dada por:
Como representa um pedaço infinitesimal do semi-anel, podemos dizer que . Substituindo isso e na expressão acima, onde , teremos:
Agora é só organizar e resolver esse cara:
Passo 2
Calcule o vetor força elétrica que age sobre a carga pontual;
Vamos calcular primeiro o campo elétrico no ponto onde está a carga, pois:
O negócio aqui é o seguinte... vamos calcular o campo elétrico a partir de um pedaço infinitesimal do fio de carga .
O campo elétrico gerado pela carga infinitesimal é dado por:
Sabendo que:
Podemos reescrever esse cara como:
Vamos analisar graficamente a situação aqui:
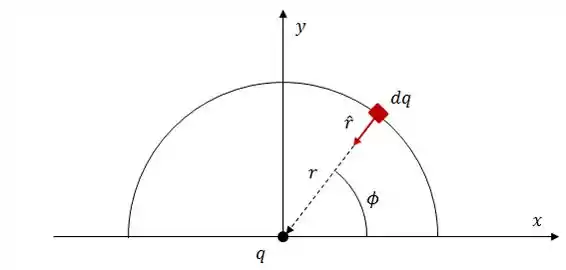
Daqui podemos tirar algumas coisas...
Passo 3
Agora sim... substituindo tudo isso na expressão de , teremos:
Antes de cair dentro das contas, vamos dar uma arrumada nessa bagunça:
Sim, eu estou ciente de que esse é um momento que bate um certo desespero... você começa a se perguntar se está fazendo a coisa certa da sua vida e tal...
Mas relaxa!
As respostas para essas duas integrais estão no seu formulário! Então se quando você estiver fazendo a prova, cair em integrais que vão te dar trabalho pra resolver, dá uma olhada no formulário da prova e vê se ele vai salvar a sua vida.
Continuando, seguindo as respostas no formulário:
Como , substituindo os valores, no final, teremos:
Passo 4
Finalmente, a força resultante sobre a partícula será:
Passo 5
Suponha que o anel é mantido fixo na sua posição e a partícula é liberada a partir do repouso. Qual será o módulo da velocidade da partícula quando ela se encontrar muito longe do anel?
No ponto inicial da partícula, ela possui uma certa energia potencial . Quando ela é liberada, ela começa a se afastar do anel e, quando , toda a energia potencial se transforma em energia cinética.
Logo, para determinarmos a velocidade da partícula quando , basta fazer:
Agora o trabalho então é calcular a energia potencial do semi-anel no ponto inicial da carga.
Passo 6
O princípio aqui é o mesmo, vamos partir de um pedaço infinitesimal de carga para calcular o potencial .
Como , teremos:
Assim, a energia potencial da carga será:
Finalmente, a velocidade será:
Resposta