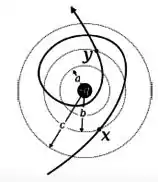
Na figura abaixo, temos uma carga puntiforme fixa de carga . A figura mostra três círculos de raios , e . Os pontos e pertencem a trajetória de uma partícula de carga . O trabalho realizado no trecho é:
Passo 1
Bom, para começo de conversa, precisamos nos lembrar de como é o campo elétrico produzido pela carga . A gente sabe que esse campo depende de , mas também depende do inverso do quadrado da distância da carga até o ponto onde queremos calcular o campo, beleza?
Então, olha na figura e repara que todos os pontos sobre cada um dos círculos possui o mesmo valor do campo elétrico, já que estão à mesma distância de . Isso significa que a carga colocada no ponto X sente a mesma força que ela sentiria se estivesse no ponto Y.
Até aqui, tudo bem?
Passo 2
Uma característica fundamental da força eletrostática é que ela é uma força conservativa. Isso significa que o trabalho realizado por essa força depende apenas dos pontos inicial e final da partícula sobre a qual se está realizando trabalho, independentemente do caminho que essa partícula segue ao sair de X e chegar em Y.
Se a partícula sai de X e segue um caminho todo bizarro, mas chega no ponto Y, esse trabalho é exatamente o mesmo que o trabalho que seria realizado se ela tivesse seguido uma linha reta saindo de X e indo até Y. Pegou essa ideia? Nos dois casos, no caminho bizarro ou na linha reta, o trabalho realizando pela força é o mesmo, já que nos dois caminhos os pontos de partida e de chegada são os mesmos.
Essa característica de campos conservativos é muito importante...Fica ligad@ nisso!
Passo 3
No nosso caso aqui, a partícula vai sair do ponto X e vai ser levada pela força eletrostática até o ponto Y. Mas repara lá na figura que esses dois pontos estão a mesma distância da carga e são, nesse sentido, “pontos iguais”. Ou seja, sai do ponto X e vai para o “ponto X”.
Por isso, independentemente do caminho que percorra, o trabalho vai ser igual a zero nesse caso, já que o ponto Y é “igual ao ponto X” . Então, o que a gente tem é o seguinte
ou seja, o trabalho realizado pela força eletrostática para levar de X até Y é ZERO!!!
Resposta
Letra d.