Unicamp – Física 3 2020.2 – P1 – Questão 3
Esse enunciado utiliza os dados de matrícula dos alunos, mas nós do RA adaptamos para você!
https://www.compadre.org/Physlets/electromagnetism/prob25_5.cfm
O objetivo deste problema é calcular a massa desconhecida da partícula vermelha. As linhas verticais representam superfícies equipotenciais. Ao deslocar a partícula (posicionando o mouse sobre a mesma e mantendo o botão da esquerda apertado) é possível obter informação sobre a sua posição (em metros (m)) e o valor do potencial nessa posição (em Volts (V)). Na animação são mostrados o valor do tempo (segundos (s)) e o valor da velocidade da partícula (m/s).
- Preencha os itens pedidos abaixo, considere que :
- Utilizando , registre a coordenada , o potencial e a velocidade para esse ponto; Tire print da tela mostrando essa posição e respectivas grandezas.
- Deixe a simulação correr até um determinado ponto de sua escolha e registre novamente as grandezas.
- Calculem o valor da massa da partícula. Expliquem seu raciocínio em detalhes. Não pulem passagens.
Passo 1
Fala galera, tudo bem? Vou ajudar você aqui!
Letra (a):
Utilizando o link fornecido (
https://www.compadre.org/Physlets/electromagnetism/prob25_5.cfm) as grandezas iniciais são:
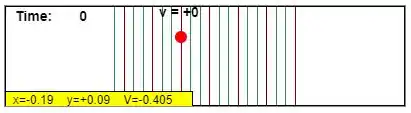
E deixando correr um pouco, foi feito novamente o registro:
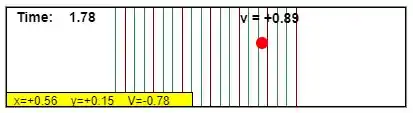As grandezas obtidas foram:
Beleza?
Passo 2
Pela equação de energia temos:
A energia cinética inicial é zero, então , a fórmula da energia potencial é , então agora é só substituir: