Halliday - Vol. 3 – 9º edição – Capítulo 24 – Seção 11 – Exercício 44
(Capítulo 24.11 – Exercício 44) Na figura abaixo, sete partículas carregadas são mantidas fixas no lugar para formar um quadrado com 4,0 cm de lado. Qual é o trabalho necessário para deslocar para o centro do quadrado uma partícula de carga +6e inicialmente em repouso a uma distância infinita?
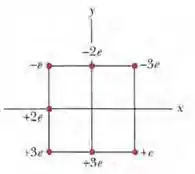
Passo 1
Fala pessoal, tudo belezinha?
Nesse exercício, temos 7 partículas carregadas, e aí queremos calcular o trabalho necessário para mover uma partícula de carga de uma distância infinita até o centro do quadrado
Caaalma hahaha é mais simples do que parece
O trabalho que a gente tem que realizar é a mesma coisa que a variação de energia potencial
Essa variação que queremos calcular aqui é da partícula que está a uma distância infinita inicialmente e queremos deslocar ela para o centro do quadrado.
Aqui usaremos a equação do potencial para resolvermos o problema.
E como só teremos energia potencial elétrica no início e no fim, lembrando que energia potencial elétrica é dada por:
Logo, teremos que:
Teremos então que calcular dois estados, inicial e final para a partícula
Passo 2
Vamos começar avaliando o que acontece no ínicio, quando a distância da partícula é infinita. Dá uma olhada aqui na voltagem inicial.
Se temos que (lembrando que uma constante sobre infinito tende a 0)
Então, nesse caso só vai interessar pra gente o final, e onde essa partícula foi parar no final? No centro do quadrado!
Passo 3
Então, pensando no final, que a partícula vai pro centro do quadrado:
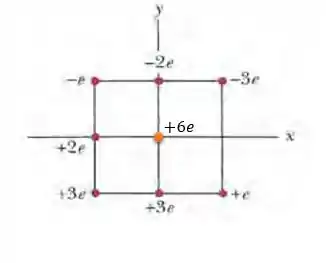
Nesse caso a voltagem aqui no ponto central será a combinação das voltagens de todas as cargas.
E lembra que o trabalho é a variação do potencial multiplicado pela carga?
A carga que realiza esse trabalho é ninguém menos que a carga e portanto ficamos com essa configuração aqui:
Passo 4
Vamos substituir os valores da figura na equação:
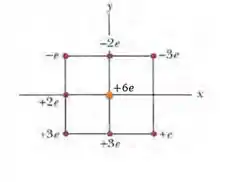
Ah um detalhe importante é que temos cargas distantes de e cargas nas diagonais distantes de , sabendo disso a equação fica com essa cara:
Somando tudo temos:
Agora aqui é basicamente substituirmos as constantes e :
Encontramos o trabalho necessário!
Ufa!!