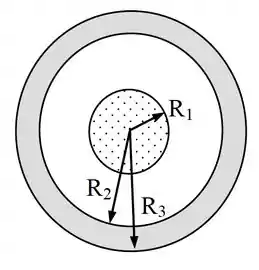
Uma esfera isolante maciça de raio possui uma densidade de carga não uniforme dada pela expressão : onde é desconhecida. Esta esfera isolante é concentricamente circundada por uma fina casca esférica condutora com raios interno e externo , como mostrado na figura.
O fluxo elétrico através de uma superfície esférica gaussiana de raio vale . Sabendo que a carga líquida depositada na casca esférica vale :
Calcule o valor da carga total da esfera maciça interna.
Calcule o valor da constante com as unidades.
Calcule a razão entre as densidades de carga interna e externa da casca esférica condutora.
Utilizando a lei de Gauss, calcule o vetor campo elétrico na região .
Calcule a diferença de potencial (), com sinal, entre a esfera interna e a casca esférica.
Passo 1
Para determinar a carga da esfera isolante, vamos precisar da linda, Lady Gauss, sabemos que:
No caso da gaussiana descrita, temos:
Sabendo que a carga líquida da casca esférica condutora é , temos que a carga da esfera isolante é:
Passo 2
Agora que sabemos quanto vale a carga total da esfera, podemos determinar a constante , pois:
Substituindo, temos:
Passo 3
Para calcular a razão entre as densidades superficiais, precisamos determinar a carga disposta na superfície interna. Para isso vamos utilizar a Lei de Gauss, lembrando que o campo elétrico no interior de um condutor é nulo. Portanto, para uma gaussiana esférica de raio , onde , temos:
Desse modo:
Onde a carga interna é a soma da carga da esfera isolante com a carga disposta na superfície interna:
Agora que temos a carga, fica fácil determinar a densidade superficial:
Como sabemos a carga da casca esférica, e sabemos a carga disposta na superfície interna, fica fácil determinar a carga disposta na superfície externa, se liga!
A densidade superficial externa será:
Agora é só calcular a razão entre as densidades:
Passo 4
Para determinar o campo elétrico na região , vamos usar a Lei de Gauss(novidade!!), temos que:
Pela simetria esférica, e pelo fato de que o vetor campo elétrico é sempre paralelo ao vetor área, temos então:
Lembrando que a carga interna será somente a carga da esfera isolante!
Passo 5
Para determinar a diferença de potencial, entre e , precisamos lembrar da seguinte relação:
Nas condições do problema, temos:
Repare que o sinal de menos do diferencial significa que os vetores são antiparalelos! Pois estamos indo no sentido contrário ao do vetor campo elétrico, que aponta para fora!
Resposta