Considere uma esfera maciça com densidade volumar de carga constante (estacionária e uniforme), raio e carga total . Qual das alternativas abaixo melhor representa os gráficos do módulo do campo elétrico e do potencial elétrico, devidos a essa esfera em função da distância ao centro?
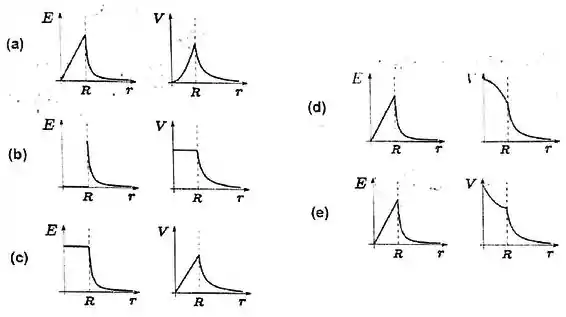
Passo 1
Como a esfera possui densidade de cargas, ela não é condutora e, portanto, seu campo elétrico no interior não é nulo, sendo então representado pela seguinte expressão:
Portanto, a primeira parte do gráfico é uma reta crescente, o que elimina as letras (b) e (c).
Passo 2
Já o campo elétrico fora é dado pela expressão:
O que mantém todas as alternativas que temos até agora
Passo 3
Analisando o potencial, temos que, por definição:
Então:
- A integral de uma reta crescente dá uma parábola, por causa do sinal negativo, fica uma parábola com concavidade pra baixo.
- A integral de uma parábola dá uma curva cúbica.
Portanto, eliminamos as letras (a) e (e)
Resposta
(d)