Unicamp, Física 3, 2019.2, P1, Questão 8.
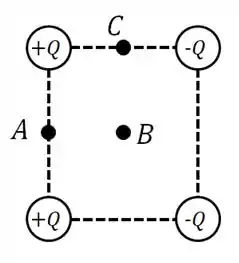
Na figura há quatro cargas puntiformes (de mesmo módulo e sinais mostrados) nos vértices de um quadrado. Considere no infinito. Em qual(is) dos pontos médios ou ) o potencial é nulo?
a) e
b) somente
c) somence
d) somente
e) e .
Passo 1
Antes de mais nada, vamos lembrar da fórmula para o potencial gerado por uma carga pontual:
Beleza. Nessa equação o é a carga e é a distância até a carga.
Pelo desenho dá pra ver que o potencial só vai ser nulo quando as cargas negativas e as positivas se cancelarem perfeitamente.
Passo 2
Vamos ver o que acontece no ponto . As linhas vermelhas representam o potencial negativo e as linhas azuis representam o potencial positivo.
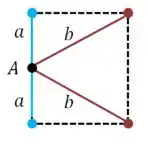
Olha o que acontece quando a gente soma as contribuições de cada um desses potenciais:
Cuidado! A gente não está fazendo uma soma vetorial (porque não estamos falando de campo elétrico, e sim de potencial elétrico). Aqui nós vamos somar algebricamente mesmo.
Beleza, o potencial não se anula no ponto .
Passo 3
Vamos fazer a mesma coisa para o ponto .
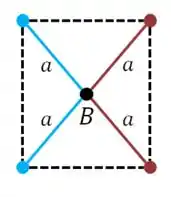
Agora todos os pontos estão à mesma distância do ponto ! O potencial total fica assim:
Então o potencial se anula no ponto .
Passo 4
E por último, vamos ver o que acontece no ponto :
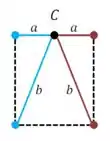
Fazendo a mesma conta de antes:
Então, resumindo tudo isso, o potencial se anula apenas nos pontos e .
Resposta
Letra (e).