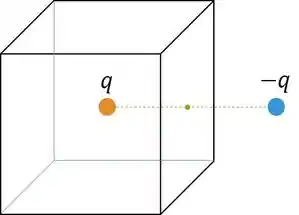
Na figura à seguir, temos duas partículas (pontuais), com carga e . Aquela de carga está envolvida por uma superfície (gaussiana) cúbica, com aresta de comprimento situando-se no centro do cubo. Um segmento de reta, também de comprimento , perpendicular a uma das faces do cubo, une as duas partículas. Para esse arranjo obteve-se: (I) o fluxo do vetor campo elétrico sobre toda a superfície gaussiana; (II) o fluxo do vetor campo elétrico sobre a face do cubo situada entre as cargas; (III) o potencial elétrico num dos vértices (ponto P) nessa mesma face. Os valores para essas grandezas são:
- , ,
- , ,
- , ,
- , ,
- , ,
- , ,
Passo 1
- Calcular o fluxo do vetor campo elétrico pelo cubo.
- Calcular o fluxo do vetor campo elétrico pela face entre as duas cargas.
Para calcular o fluxo do vetor campo elétrico, podemos aplicar diretamente a lei de Gauss:
Que diz que o fluxo do vetor campo elétrico por uma Gaussiana fechada qualquer é igual à carga no interior desta superfície dividida por . Isto significa que cargas no exterior não contribuem para o fluxo total.
Portanto a primeira grandeza é:
Pois a carga no interior do cubo é somente .
Passo 2
Aqui tem uma pegadinha. Vamos tentar calcular somente o fluxo da carga pela face pedida.
Sabemos que o fluxo total proveniente da carga é:
Mas se o cubo tem seis faces, então o fluxo por uma face só deveria ser somente um sexto deste valor! Por conta da simetria do problema isto é verdade, portanto:
Onde é a face desejada. Ok, beleza, mas não acabou aqui, pois a carga externa também faz fluxo nesta face!
Pode parecer confuso, pois o fluxo total da carga pela gaussiana (de acordo com a lei de Gauss) deveria ser zero. Isto é fato, entretanto, só porque é zero não significa que o fluxo por cada face individual tenha que ser zero. Na verdade não é. O que ocorre é que a soma dos fluxos dessa carga pela superfície é que dá zero!
Portanto, para chegar neste valor vamos usar um macete de simetria. Como as duas cargas estão dispostas de maneira simétrica e a uma distância igual com relação ao cubo, podemos dizer que o fluxo dela pela face é igual ao da carga !
Uma ilustração para essa ideia é a seguinte:
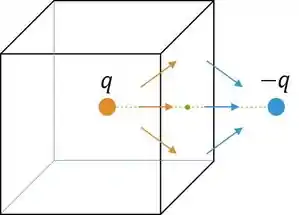
Lembrando que fluxo só pode ser calculado se você tiver arbitrado um sentido para o seu vetor . Como na lei de Gauss nós arbitramos o vetor área apontando para fora da superfície, a carga faz um fluxo positivo na face . Portanto, o fluxo total é:
Passo 2
Agora basta aplicarmos a fórmula de potencial elétrico. Não confundir com a energia potencial elétrica.
Para cargas pontuais a fórmula é a seguinte:
Onde é a distância até o ponto desejado. Como no caso a distância é a mesma tanto para quanto para , somamos:
Fim de papo.
Resposta
Letra b.