UFJF – Física 3 – AV1 – 2014.1 – Questão 1b
Três cargas pontuais se encontram nos vértices de um triângulo equilátero de lado . O centro do triângulo está na origem de um sistema de coordenadas cartesianas e o plano do triângulo fica no plano . Uma das cargas está no eixo as outras simetricamente nos quadrantes III e IV, como mostra a figura. A carga no eixo assim como a carga no quadrante IV tem o valor e a carga no quadrante IV tem o valor .
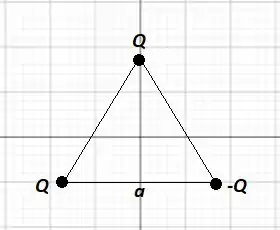
(b) Tomando o potencial elétrico no infinito como zero, calcule o potencial elétrico na origem.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá três cargas pontuais onde elas se situam em cada ponta de um triângulo equilátero (que possui lados iguais).
A questão nos pede para calcularmos o potencial elétrico gerado pelas cargas puntiformes na origem.
Lembrando que o potencial elétrico é dado da seguinte forma:
Onde é a constante eletrostática, é o valor da carga e é a distância da carga ao ponto que queremos (no caso, o centro do triângulo).
E aí? Bora responder?
Passo 2
Bom... O potencial elétrico no centro do triângulo é dado pela soma dos potenciais das três cargas puntiformes, ou seja:
Lembrando que e são potenciais de cargas positivas e , de carga negativa.
Passo 3
Dessa forma, como os potenciais são iguais em módulo, temos:
Na letra (a) descobrimos que .
Assim, temos que o potencial total do sistema é dado por:
Entendeu direitinho? Responde aee ;)
