Três partículas carregadas com cargas , e são fixadas sobre os vértices de um triângulo equilátero, como mostrado na figura abaixo. O centro do triângulo é indicado pelo ponto
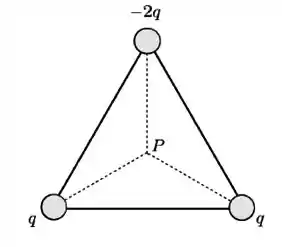
Considere que a energia potencial elétrica seja nula quando as cargas estiverem infinitamente afastadas. Sobre esse sistema, são feitas as afirmativas abaixo:
- A energia potencial elétrica do sistema é negativa.
- O potencial elétrico é constante sobre um eixo perpendicular ao triângulo e que passa por .
- O trabalho realizado pela força elétrica sobre uma partícula carregada, quando ela é deslocada do infinito até o ponto , é nulo.
São VERDADEIRAS as afirmativas:
- Nenhuma delas.
Passo 1
I) Para calcularmos a energia potencial elétrica do sistema, vamos tomar a figura a seguir com as partículas , e com cargas e , respectivamente. A energia potencial elétrica entre duas partículas quaisquer e , separadas por uma distância , é dada por
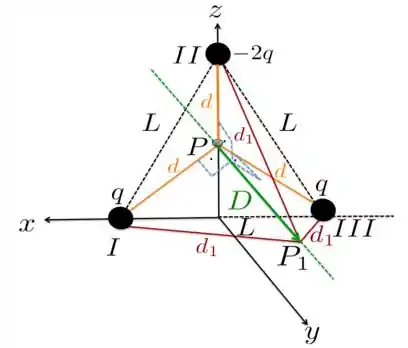
A partir dessa figura, vamos considerar apenas os seguintes pares de partículas , e . Por quê não colocamos também o par ? Porque esta energia será idêntica àquela do par , que já foi considerada. Ou seja, só precisamos contabilizar a energia de um par uma única vez.
Tendo isso mente, pessoal, a energia potencial elétrica do sistema neste caso é
que é negativa, tornando o item desta questão CORRETO.
Passo 2
II) Como o ponto da figura está no centro do triângulo equilátero, ele está situado a uma mesma distância igual de todas as cargas do triângulo, correto?
A reta que passa pelo ponto da figura é perpendicular ao plano definido pelas três cargas e um ponto arbitrário desta reta está à mesma distância de todas as três cargas, como indicado na figura. Portanto, os triângulos , e são retângulos e iguais.
Assim, o potencial produzido pelas cargas na posição de um ponto arbitrário da reta é dado por
ou seja, o potencial em qualquer ponto sobre a reta é CONSTANTE E IGUAL A ZERO! Por isso, o item II) está CORRETO.
Passo 3
III) Como o problema se trata de um sistema de cargas estáticas, então temos um sistema conservativo. Dessa maneira, o trabalho realizado pelo campo elétrico desse sistema para levar uma partícula de carga do infinito até o ponto depende apenas da energia potencial no infinito e da energia potencial no ponto
A energia num ponto a um distância arbitrário do sistema pode ser escrita como
em que é o potencial gerado pela distribuição no ponto . Então, o trabalho pode ser escrito como
Como o potencial gerado pelo sistema no infinito é zero, , e o potencial no ponto também (o potencial sobre qualquer ponto sobre a reta é constante e nulo!), então o trabalho é
Portanto, a energia gasta pelo sistema para levar qualquer partícula do infinito até o ponto é ZERO.
O item III) da questão está CORRETO.
Resposta
Portanto, o item g) está correto.