13ª questão - Você fixa quatro cargas pontuais idênticas e de massa nos vértices de um quadrado de lado . Em seguida, você as libera simultaneamente, de modo que elas passam a se afastar. A máxima velocidade que cada carga atingirá será:

A) infinitamente grande

B)

C)

D)

E)

A energia potencial compartilhada por duas partículas carregadas que interagem eletrostaticamente é dada por:

onde são as cargas das partículas e é a distância entre elas.

Mas, um detalhe bem importante aqui é que essa energia é do sistema, ou seja, não é a energia potencial de apenas uma das cargas. Na realidade, essa energia potencial se divide entre as duas cargas que estão interagindo eletrostaticamente.

Assim, considerando que a energia potencial se divide igualmente entre duas cargas que estão interagindo, podemos dizer que a energia de cada carga vale:

No caso, todas as partículas são iguais, logo e é a distância entre as cargas

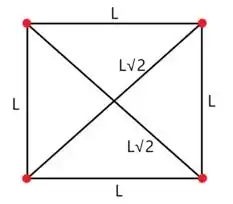
Em cada carga, a energia potencial inicial é dada como

Como é igual a , então

Quando as cargas são liberadas, a energia potencial gradualmente se transforma em energia cinética, ou seja:

Entendeu essa parte? 👀

Agora, pensa comigo, queremos calcular a velocidade máxima que a carga vai atingir.

Se a velocidade for máxima, a energia cinética também vai ser máxima, concorda?

Assim, isso irá acontecer quando toda a energia potencial se transformar em energia cinética.

Daí, igualando a energia potencial com a energia cinética, temos:

Isolando em um lado da equação, temos

Comparando o resultado que obtemos com as alternativas dadas no problema, vemos que a alternativa C) é a que condiz com nosso resultado!

É isso! Essa resolução te ajudou? Responde Aí! ✌