Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Potencial Elétrico Gerado por Carga Pontual

Ver Teoria
Exercício 981234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969799100

Enunciado

Duas placas planas e infinitas situadas nos planos z = 0 e z = a estão carregadas com densidades superficiais de carga 2 σ 0 e - 3 σ 0 , respectivamente, como mostra a figura:

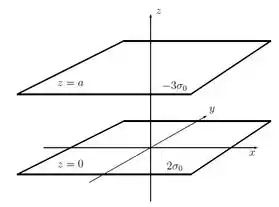
(a) Usando a lei de Gauss, calcule o vetor campo elétrico nas regiões z < 0 , 0 < z < a e z > a .

(b) Calcule a diferença de potencial entre os pontos z = a / 2 e z = 2 a .

Passo 1

a)Vamo lá, pra começar, a gente vai considerar uma placa plana infinita com densidade de carga superficial σ . Essa placa vai estar localizada ao longo do eixo z com coordenada z = d .

Vamos utilizar a Lei de Gauss para analisar o campo elétrico, sendo que a nossa superfície Gaussiana vai ser um cilindro infinitesimal, conforme mostra a figura abaixo

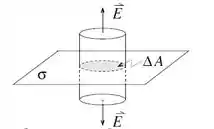
Por simetria, o campo E → é perpendicular ao plano e aponta na direção k ^ se z > d (acima do plano) e na direção - k ^ se z < d (abaixo do plano). A gente percebe pela figura que apenas o fluxo de campo elétrico nas bases do cilindro será diferente de 0 e esse fluxo só vai depender da distância até o plano.

Agora vamos supor uma área infinitesimal ∆ A suficientemente próxima do plano para podermos considerar E → constante. Nesse caso, o fluxo de campo elétrico vale 2 E ∆ A . Como q i n t = σ ∆ A temos que

ϕ = q i n t ε 0

2 E ∆ A = σ ∆ A   ε 0

E = σ 2 ε 0

Então, nosso campo elétrico generalizado vai ser o seguinte

E → = - σ 2 ε 0 k ^ ,   s e   z < d σ 2 ε 0 k ^ ,   s e   z > d

Só falta aplicar nos dados do exercício

Passo 2

Aplicando as expressões deduzidas para σ = 2 σ 0 e σ = - 3 σ 0 e com ajuda da figura do enunciado, a gente consegue concluir que

E 1 → = - σ 0 ε 0 k ^ ,   s e   z < 0 σ 0 ε 0 k ^ ,   s e   z > 0

E 2 → = 3 σ 0 2 ε 0 k ^ ,   s e   z < a - 3 σ 0 2 ε 0 k ^ ,   s e   z > a

Então o campo elétrico total, pelo princípio da superposição, vai ser

E t → = E 1 → + E 2 → = σ 0 2 ε 0 k ^ ,   s e   z < 0 5 σ 0 2 ε 0 k ^ ,   s e   0 < z < a - σ 0 2 ε 0 k ^ ,   s e   z > a

Passo 3

b)A diferença de potencial entre os pontos a e b é dada por

V b - V a = - ∫ a b E → . ⅆ l →

O campo elétrico é diferente nas regiões a 2 < z < a e a < z < 2 a não é? Então a gente vai dividir a integral em duas partes, vai ficar assim

( V 2 a - V a ) + ( V a - V a / 2 ) = - ∫ a / 2 a E → . ⅆ l → - ∫ a 2 a E → . ⅆ l →

Como o campo é constante em cada uma das regiões, a integral vai ser resolvida como constante e aí as expressões ficam assim:

V 2 a - V a = - a k ^ . - σ 0 2 ε 0 k ^ = a σ 2 ε 0

V a - V a 2 = - a 2 5 σ 0 2 ε 0 = - 5 2 a σ 0 2 ε 0

Logo, temos que

V 2 a - V a / 2 = - 3 2 a σ 0 2 ε 0

Resposta

  1. E t → = σ 0 2 ε 0 k ^ ,   s e   z < 0 5 σ 0 2 ε 0 k ^ ,   s e   0 < z < a - σ 0 2 ε 0 k ^ ,   s e   z > a
  2. V 2 a - V a / 2 = - 3 2 a σ 0 2 ε 0

Exercícios de Livros Relacionados

Considere uma carga pontual q = 1,0 μC, o ponto A a uma distância d 1 = 2,0m de q e o ponto B a uma distância d 2 = 1,0m de q. (a) Se A e B estão diametralmente opostos, como na figura da esquerda aba
A figura (a) mostra duas partículas carregadas. A partícula 1, de carga q 1 , é mantida fixa no lugar a uma distância d da origem. A partícula 2, de carga q 2 , pode ser deslocada ao longo do eixo x.
Na figura (a), uma partícula de carga +e está inicialmente no ponto z = 20 nm do eixo de um dipolo elétrico, do lado positivo do dipolo. (A origem do eixo zé o centro do dipolo.) A partícula é desloca
A figura (a) mostra três partículas no eixo x. A partícula 1 (com uma carga de +5,0 μC) e a partícula 2 (com uma carga de +3,0 μC) são mantidas fixas no lugar, separadas por uma distância d = 4,0 cm.
Um pósitron (carga + e , massa igual à do elétron) está se movendo com uma velocidade de 1 , 0 · 10 7m / s no sentido positivo do eixo x quando, em x = 0 , encontra um campo elétrico paralelo ao eixo