Campo Elétrico, Potencial Elétrico
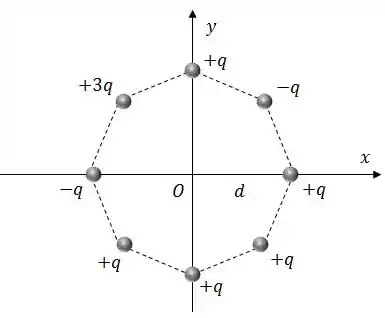
Calcule o campo elétrico no ponto devido à distribuição octogonal de cargas na figura (use o sistema de coordenadas indicado);
Calcule o potencial elétrico em ;
Qual será a aceleração instantânea adquirida por uma partícula de massa , carregada com uma carga positiva , abandonada em ?
Passo 1
Calcule o campo elétrico no ponto devido à distribuição octogonal de cargas na figura (use o sistema de coordenadas indicado);
Vamos começar dando nome às cargas:
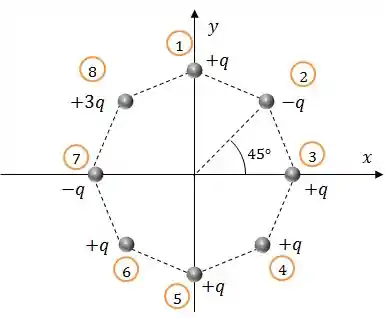
O campo elétrico resultante será a soma vetorial dos campos elétricos gerados por cada carga.
O campo elétrico gerado por uma carga é dado por:
Passo 2
Vamos esboçar o campo gerado por cada carga:
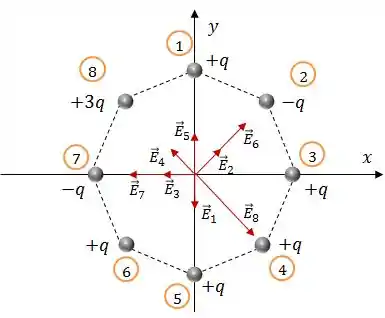
Esses campos serão dados por:
Assim, o campo elétrico resultante será:
Passo 3
Calcule o potencial elétrico em ;
O potencial gerado por uma carga em um ponto a uma distância é dado por:
Então só temos que somar os potenciais gerados pelas 8 cargas no ponto :
Passo 4
Qual será a aceleração instantânea adquirida por uma partícula de massa , carregada com uma carga positiva , abandonada em ?
Já calculamos o campo elétrico na letra , certo? A força elétrica sobre uma carga , no ponto está associada ao campo elétrico por:
Ou, como estamos trabalhando só com o módulo do campo:
Além disso, de acordo com a Segunda Lei de Newton:
Logo:
Resposta