O potencial elétrico de uma placa de vidro muito grande é . Ela tem uma distribuição de carga positiva e uniforme sobre sua superfície com uma densidade .
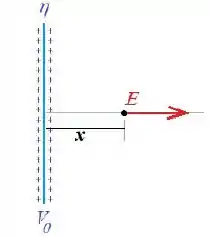
Determine o potencial a uma distância da placa. Considere que o ponto está longe das bordas e que é muito menor que as dimensões da placa.
Passo 1
Pra calcular o potencial, precisamos lembrar que o campo elétrico gerado por uma placa infinita é dado por:
Passo 2
A diferença de potencial entre dois pontos e o campo elétrico estão relacionados da seguinte forma:
Como o campo elétrico está na direção do eixo , temos que:
Essa equação calcula a diferença de potencial entre dois pontos. Dessa forma, para calcular o potencial a uma distância da placa, precisamos partir de um ponto no qual saibamos quanto vale o potencial.
Aqui, vale lembrar que o problema nos disse que o potencial da placa é , então vamos esse como nosso ponto inicial. Assim:
Assim, a resposta certa é a letra .
Resposta