UFRJ- Física 3 – PF 2018.2 - DIURNO - 6
Duas partículas de cargas e estão separadas por um distância , como mostra a figura abaixo. Nessa situação, podemos afirmar que o trabalho realizado pela força elétrica para trazer uma terceira partícula de carga do infinito para o ponto indicado na figura vale:
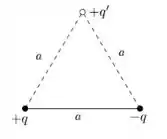
- 0
Passo 1
O trabalho realizado pela força elétrica para trazer a carga do infinito até o ponto do vértice do triângulo equilátero é dado por
sendo que é o potencial total gerado pelas cargas e na posição do vértice do triângulo equilátero e é o potencial que essas cargas geram no infinito.
Como o potencial gerado por uma carga pontual num ponto a um distância é dado por
então, o potencial no infinito é nulo: .
Portanto, para calcularmos o trabalho, basta vermos como é o potencial gerado pelas cargas no ponto onde está a . No entanto, como as cargas têm sinais opostos e estão à mesma distância de :
Isso implica, portanto, que o trabalho realizado pela força elétrica é
Resposta
Letra e).